# Animation(动画)
这一节涉及到计算机动画相关的知识,我们会讲到动画的历史、一些基本的制作动画的方法、物理模拟一些基本的思想、运动学以及绑骨相关的知识。

动画,作为一种交流的工具,给别人展示各种各样动起来的东西,并且动画更关注于美学上好不好看。在图形学中,也可以把动画理解成对于建模或者是几何上的拓展,无非就是在不同的时间它们有不同的几何形状,而为了得到这些几何形状,就会想要怎么去做,怎么去计算,算出来之后再在每一帧去播放它对应的图,相当于我们把 3D 的一张图延伸到了时间的维度上面去。动画的形成是由很多的图按顺序、按一定的速度去播放它就可以了,因为人眼有视觉暂留的效应,这也说明了我们不需要在整个时间范围内非常集中的去采样。对于电影来说,每一帧播放 24 张图,也就是 24fps,我们平常播放的一些视频可能是 30fps,对于虚拟现实,为了让人看上去不晕,就需要达到 90fps,这也说明,对于不一样的应用来说它们对动画的要求也是不一样的。
# Historical Points in Animation

早期的动画是远古的人类在墙壁上画的各种各样不同的图,如果我们把这些图截下来然后按顺序播放,就可以看到一段动画。那时的人类就已经明白,动画无非就是在不同的时间用不同的图,然后把他们播放出来,只不过那时候并没有播放设备而已。

后来,又有些类似圆盘的物体,通过旋转圆盘,人们可以看到一段循环播放的动画。

到了科学有了一定发展程度的阶段,人们开始真正发明了电影的技术,不过最早期的电影技术并不是用来娱乐的,而是当作科学的研究设备,例如上面就是用电影去拍一匹奔跑的马,我们可以研究在任何一个时间点下马的四肢是一种什么样的摆放,由此可以把生物学的一些问题给研究明白。只不过随着发展渐渐发现人们非常喜欢看这些动态的东西,于是电影业就慢慢的变成了娱乐业。







# Keyframe Animation
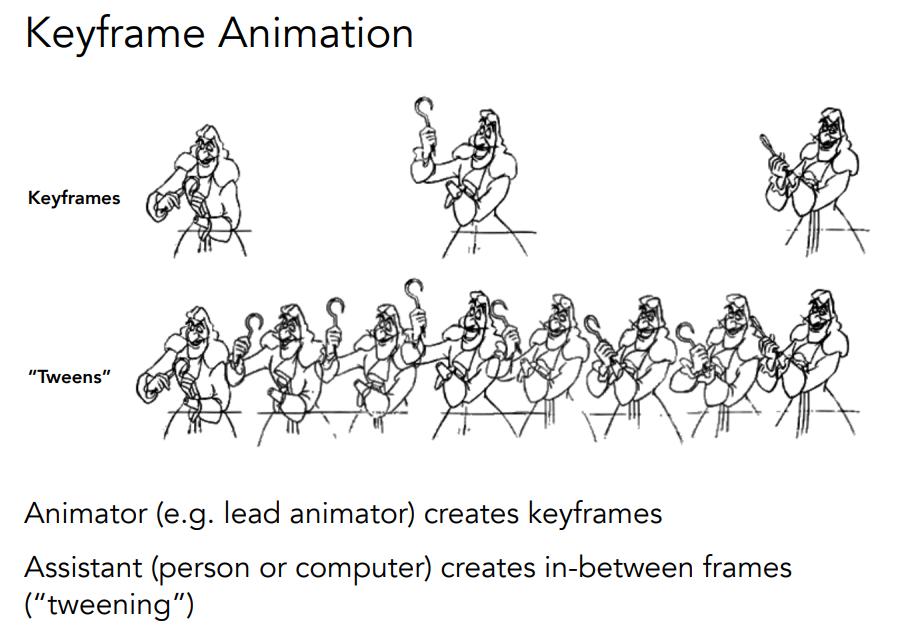
简单了解了动画的历史之后,接下来我们来看动画是怎么制作出来的。首先我们提到的一种技术就是关键帧动画。关键帧很好理解,观察上面这幅图,这个人物在三个不同的时间有三个不同的动作,通过在这三个动作之间插值去补充过渡的一些动作从而形成一段动画,而那三个定义了动画走向的动作就被称之为 “关键帧”。早期制作关键帧动画是一个费时费力的过程,最厉害的那些艺术家们会画出关键帧,然后再由助手们帮忙把中间的帧给画出来,直到现在漫画家们画出来的那些漫画,如果要做成动画一定也是要投入大量的人力去把中间那些过渡的过程给画出来。
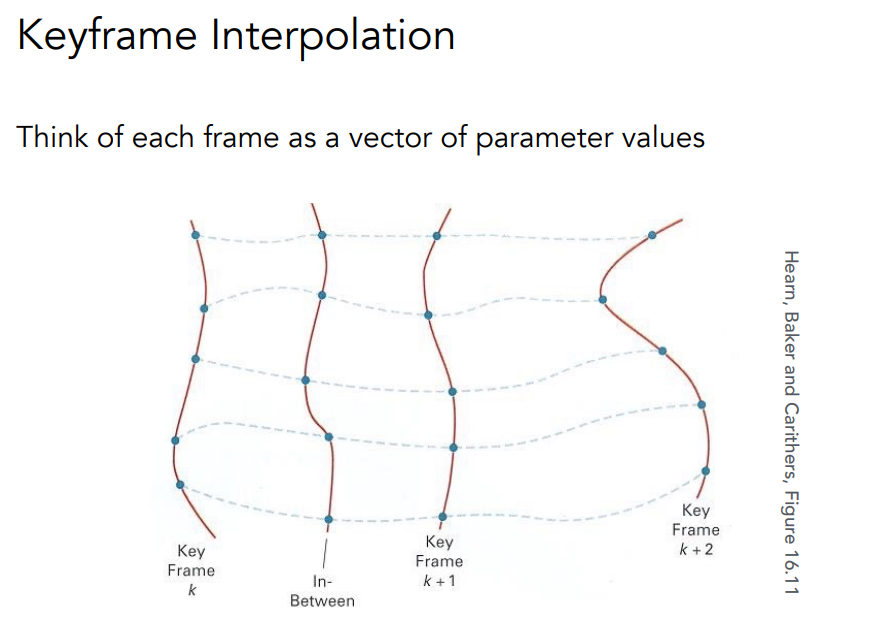
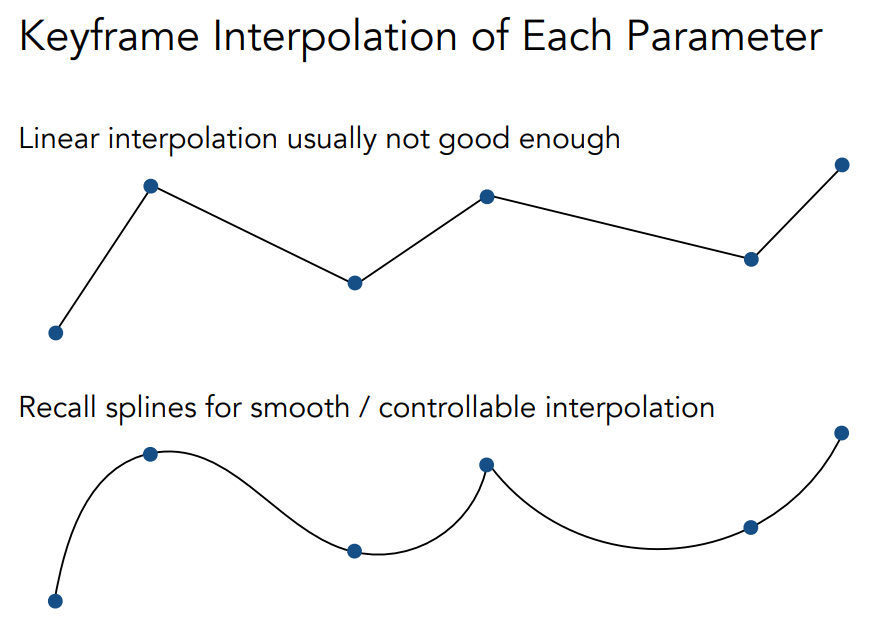
对于那些自动进行补帧的动画,关键帧之间的插值就是一门学问,有最最简单的线性插值,而插值怎么样能让动画看起来更自然、更真实就很有讲究了。
# Physical Simulation
我们刚才说关键帧动画是一种比较简单的做法,中间的过程就是插值,只不过是认为的方式还是自动的方式,更多的情况下人们用的是物理仿真的方式去做的。
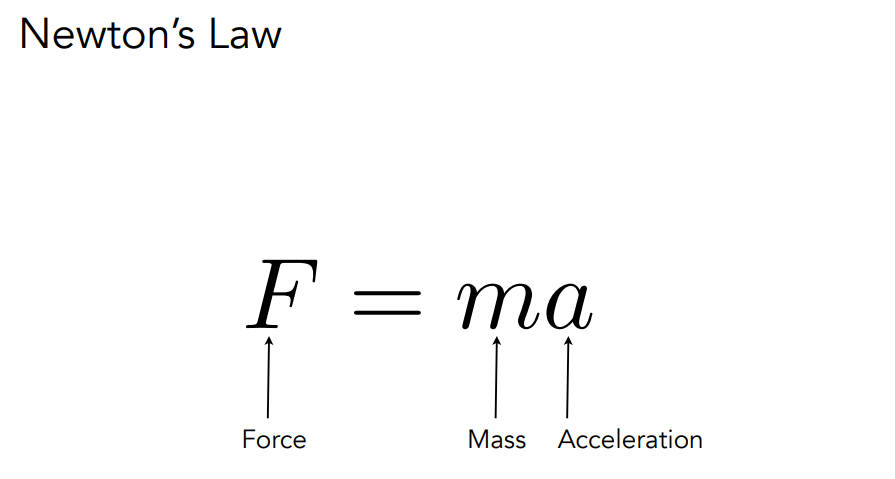
最简单的大家都知道的物理,我们会提到牛顿运动定律。物体有质量 m,应用在物体上有一个力 F,然后这个物体就会获得一个加速度 a,它们之间的关系就是。有加速度我们就能算速度,有速度就可以算位置,也就是说我们只要直到了物体上有什么样的力以及它的一些初始的运动条件,我们就能动态的更新这个物体在下一个时刻的位置。物理仿真就是在推导各种不同的物理公式来计算出物体的变化过程。

一个上抛的小球受到重力会向下掉落,这是一种简单的情况,而对于右边的衣服来说,它是由许多网格形成的,我们可以认为任何一个顶点上它有一个质量,它会受到重力,同时它因为和其他的顶点相连,它也会受到来自其他顶点的各种作用力,虽然它很复杂,但如果我们把所有的力都考虑进去,自然也可以算出它的加速度,算出来之后自然也可以更新它的速度和位置,只要我们能够正确地把它受力的模型给构建出来,这就是物理仿真背后的思想。

上面这个例子是一个布料的模拟。当人物在运动的时候,衣服也会跟着一起运动。这当然是因为中间会有摩擦力、压力等等各种各样的力在作用。当把各种各样的力都算出来之后自然而然就可以得到正确的结果。如果模拟的不好,会出现穿模的问题。解决这个问题就涉及到碰撞检测的一系列算法。但只要能够正确建立它的物理模型,自然可以通过解一定的方程把它给算出来。

另一个例子是流体的例子,上面这张图是对水的模拟。看待这种问题通常分两步看,第一步模拟水是怎么运动的,它的水滴以及各个部位是怎样形成的。当我们模拟了它的位置、形状各种东西之后,我们会进行渲染,才能看到它长什么样。通常我们并不会去关心它的渲染应该怎么做,而是去关心例如它水花四溅是怎么模拟出来的。
# Mass Spring System: Example of Modeling a Dynamic System
我们既然已经提到了只要正确的建立物体之间的相互作用力,自然而然就可以模拟正确的效果。这里给大家介绍一套最简单且实用的一套系统,叫做质点弹簧系统。下面是质点弹簧系统应用的几个例子。

上面这个例子是课程的第八次作业 —— 绳子模拟器。我们可以把一根绳子模拟成很多小弹簧连接在一起。之后可以让它在重力的作用下来回摆动、甚至还可以拖动它。

上面是对头发的模拟。我们这里和上面一样,还是把渲染和物理仿真两个部分分开看。这里我们并不关心怎么才能让头发渲染的真实,而是头发在各种不同的作用力下它会有怎样的变化。
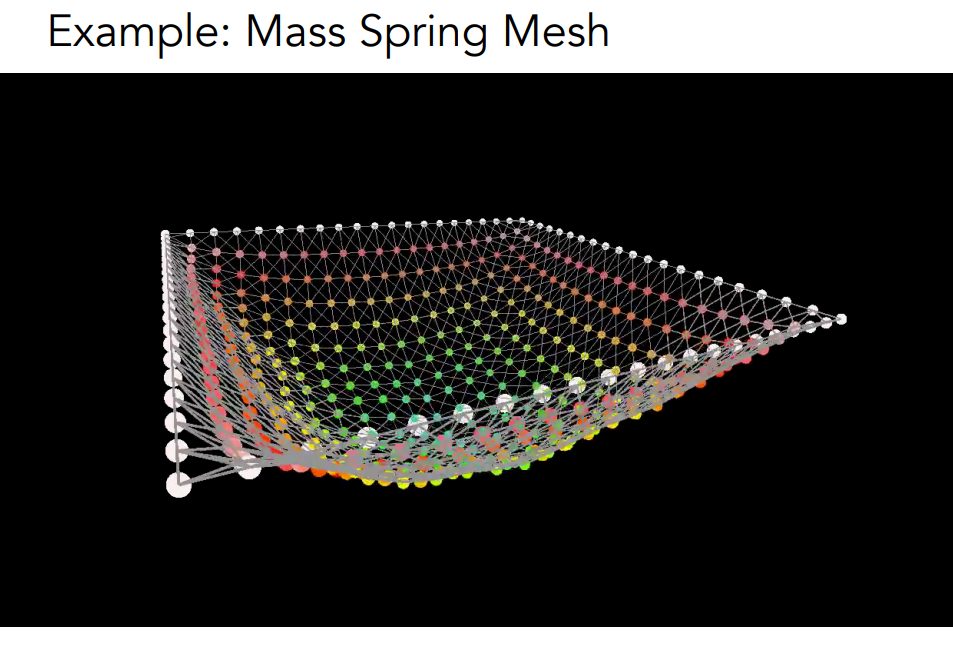

质点弹簧系统还可以进行布料模拟。布料本身是由网格来描述的,很自然的就可以用质点弹簧系统来描述它。上面这个例子就说明了,如果对于一块布只要建模的足够好,那么模拟的仿真是完全可以达到以假乱真的效果的。

现在让我们回到质点弹簧系统上。质点弹簧系统指的是一系列相互连接的质点和弹簧。它的最基础的单元就是一个弹簧左右连接着两个质点。我们先假设一个理想化的弹簧没有长度,它被拉开了多长就表明它会产生多大的力。上图从 a 到 b 的作用力可以通过 b-a 得到的向量乘劲度系数得到,这个定律也叫做胡克定律。由于力的作用是相互的,质点 a 受到向右的力,因此质点 b 受到一个向左的力,它们互为相反。

前面我们使用的公式很明显存在一个问题,即不存在长度为 0 的弹簧。弹簧在正常情况都应该有一个长度,这个长度叫做 Rest Length(静止长度:指弹簧或其他弹性物体在没有受到外力作用时的自然长度),这里我们表示成 l 。那么我们的公式可以更新成上面这种形式。但是还是存在问题,当弹簧产生力的时候,它会永远的震动下去,因为能量守恒。这里动能和势能永远都在持续一个转换的过程。怎么解决呢?那么我们就加入一个摩擦力,让它能够停下来。

在这之前我们先引入一个在物理仿真和模拟中经常使用的记法,即在符号上打一个点表示一阶导数,打两个点表示二阶导数。

我们刚才说弹簧永远都会震动,但我们不希望这样,于是我们就给它加一个摩擦力让它能够停下来,这里我们称之为 damping(阻尼)。既然阻尼会让它停下来,那么这个力作用的方向肯定是和它速度的方向相反的。对于任何一个质点,它的速度 乘上一个系数 并且取反作为我们的阻尼力。但是它还是有一个问题,就是它会让所有的运动都停下来。假设我们有一个弹簧左右质点 a 和 b,如果 a 和 b 同步的向右走,会出现弹簧并没有拉伸产生震动,但是最后却会停下来。也就是说,我们描述的这个阻尼只能描述外部的力,描述不了弹簧之间内部的这种力。

那么怎么办呢?我们刚才提到 a 和 b 同步运动,也就是说其实这个内部的摩擦力应该是和它们之间相对运动有关系。那么,我们首先要考虑的一个东西就是这个内部的摩檫力它要做一个什么事,它最终是希望弹簧会恢复到它最初的长度。也就是说,只要 a 和 b 被拉开了,那么 a 肯定会想办法向 b 方向去靠。因此,如果 a 和 b 之间被拉开了,a 应该会受到一个向右的力,b 应该会受到一个向左的力。以 b 受到的力为例,它可以用上面这个表达式进行表达(红色框的区域代表的是向量点乘,表示的是 a 和 b 之间的相对速度投影在 a 到 b 的方向上的速度大小)。为什么我要要做这个投影呢?因为相对速度本身还解决不了问题,因为有一些速度并不能引起弹簧长度上的改变。例如,当 a 点被固定,让 b 点绕 a 点做圆周运动时,这里就会出现问题,因为这个时候 b 的速度是垂直于弹簧的,这个时候它的速度是绝对不应该引起弹簧本身内部的摩檫力让它损耗后停在它的自然长度上的。因此,我们这里需要做一个点乘,也就是把相对速度分解到沿着 ab 方向,这个方向的相对速度才会对整个弹簧振子系统造成所谓的衰减。
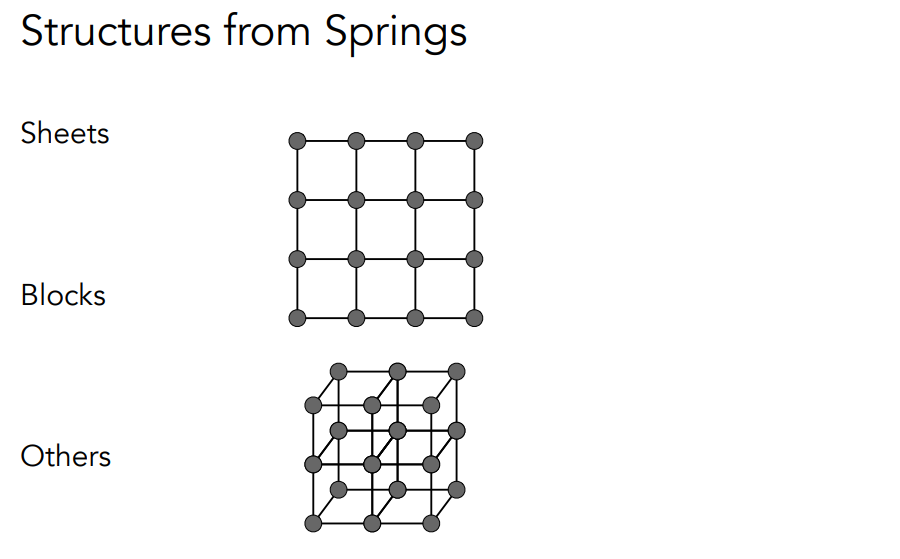
我们既然已经讨论了一节弹簧连着两个质点的情况,那么我们自然而然就会考虑它们各种各样不同的组合形成的更加复杂的形状。
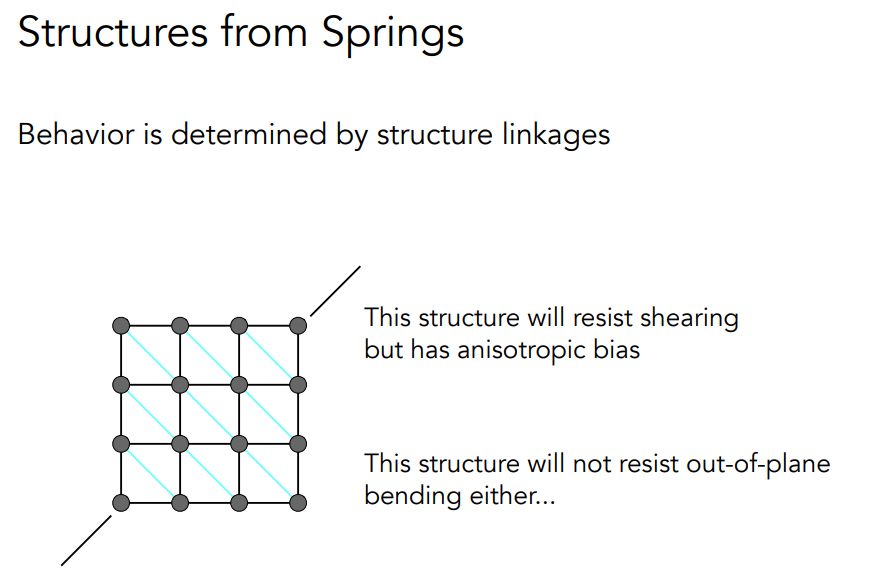
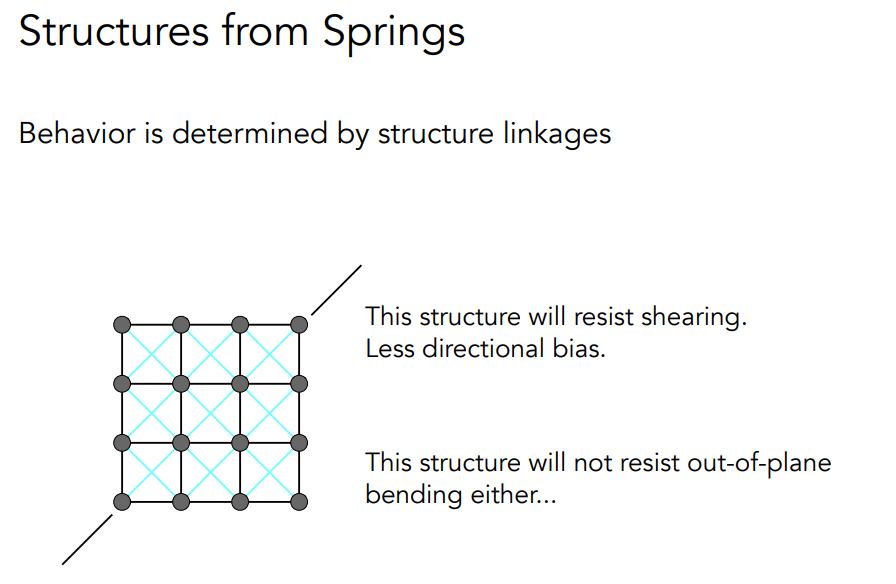
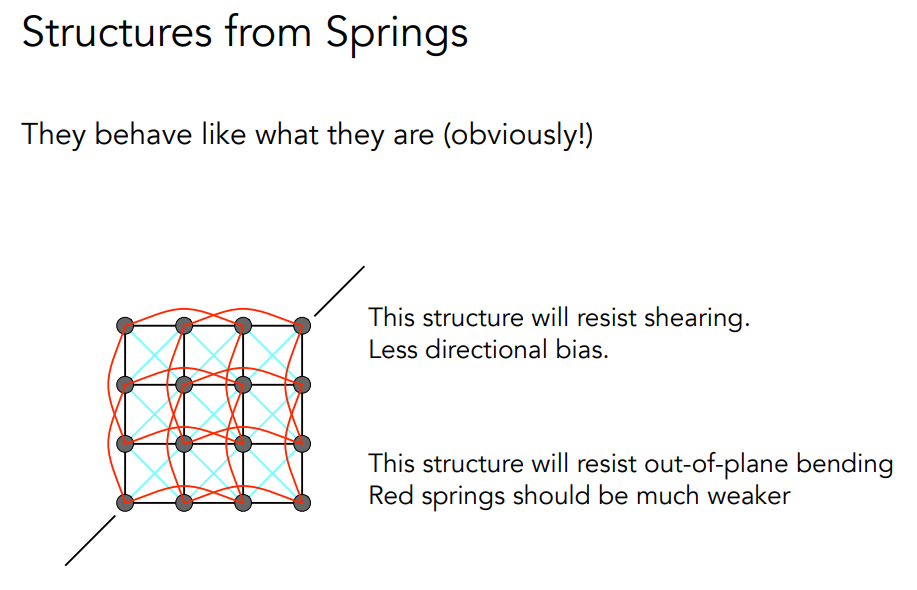


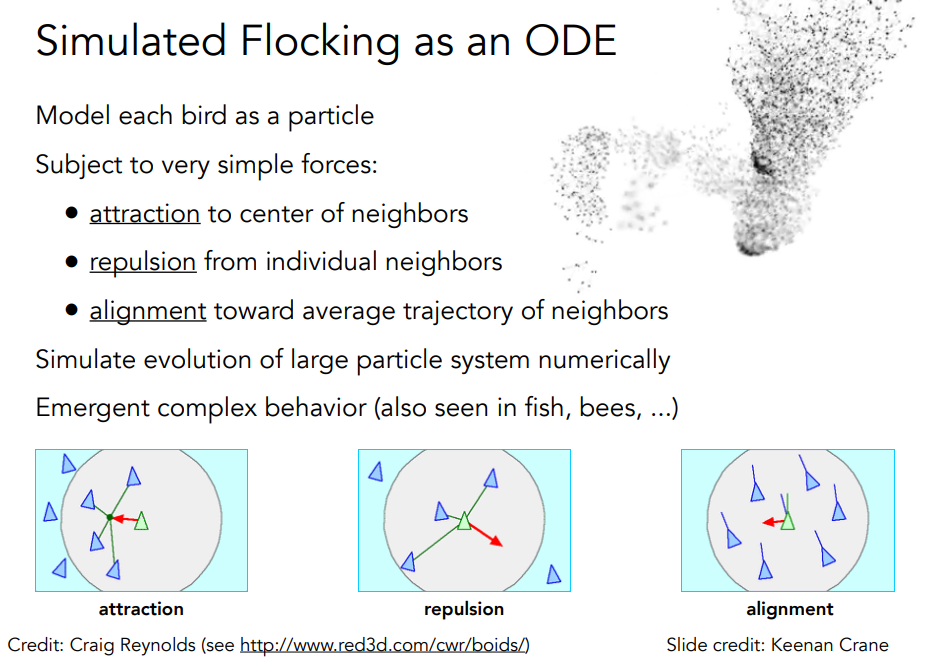
# Particle Systems








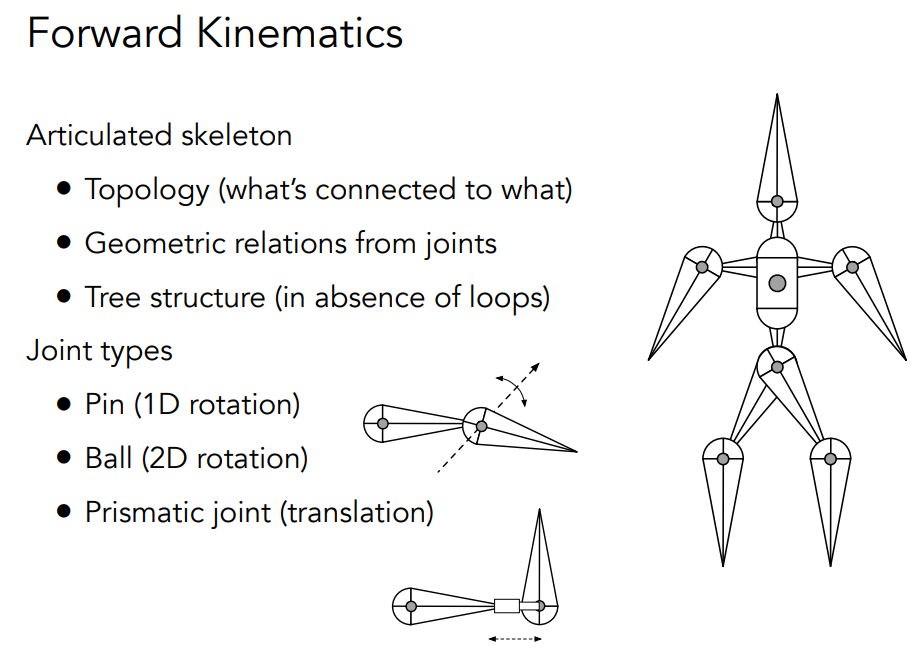
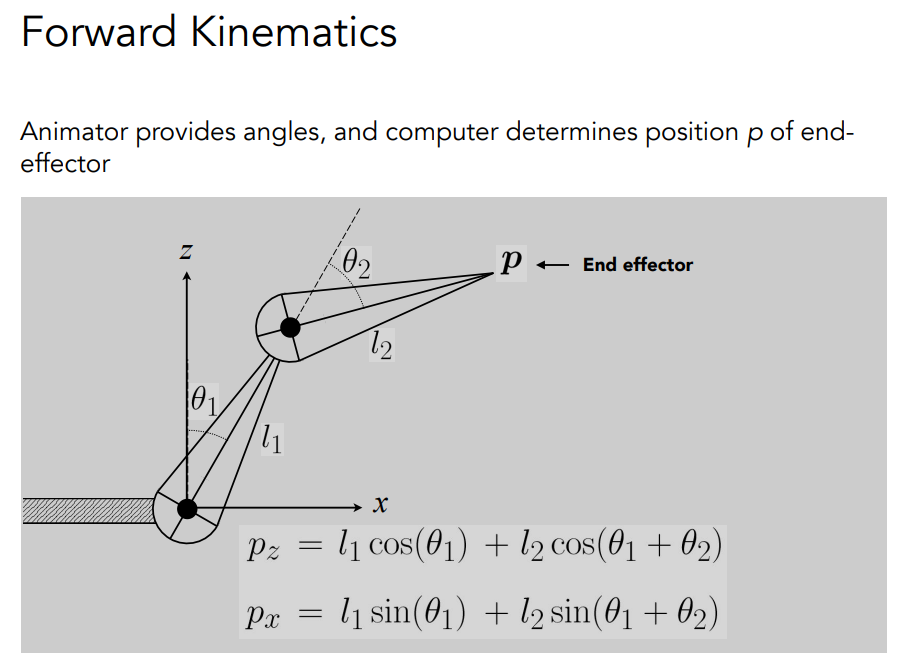
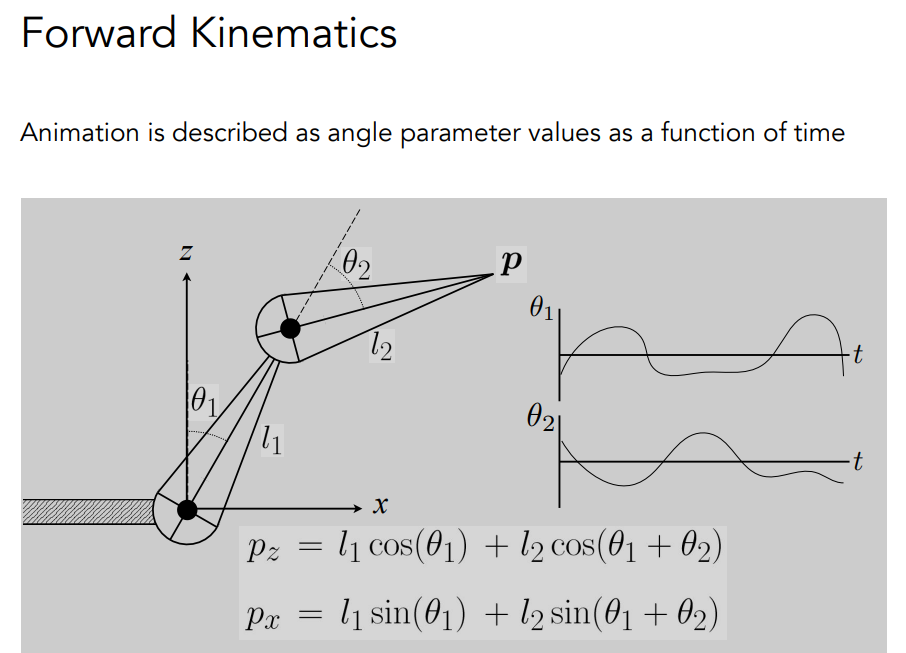
# Forward Kinematics
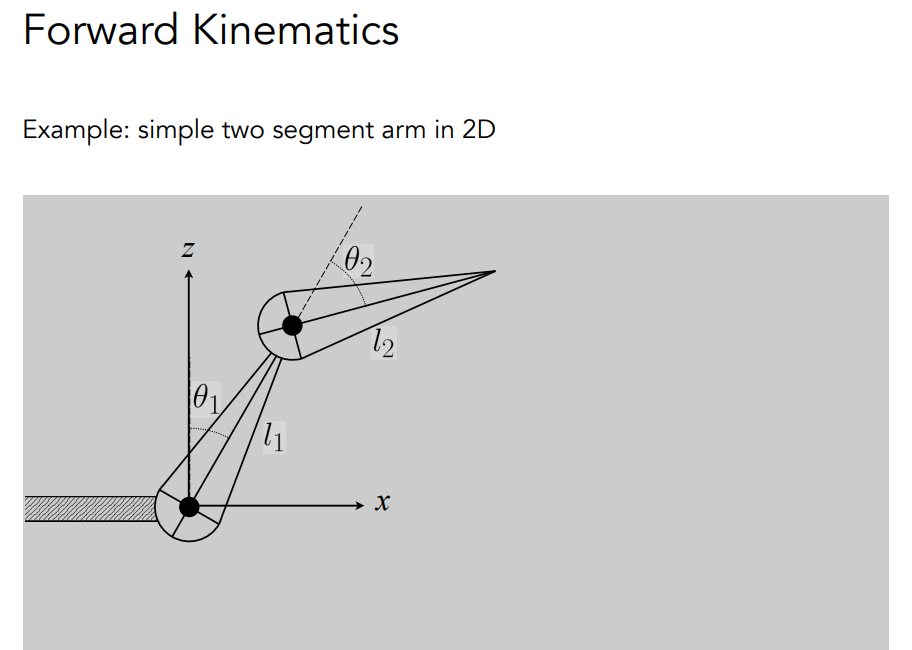

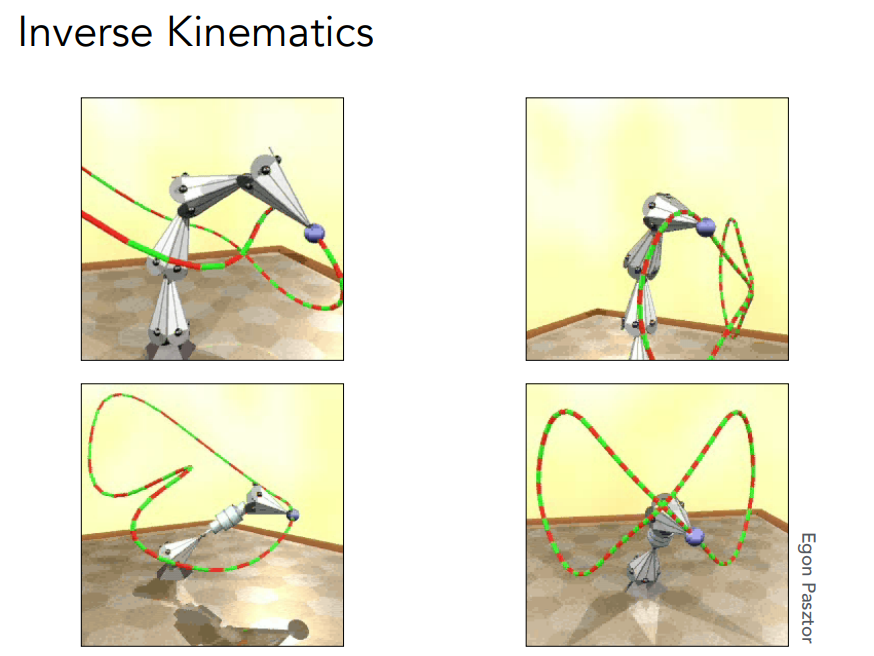
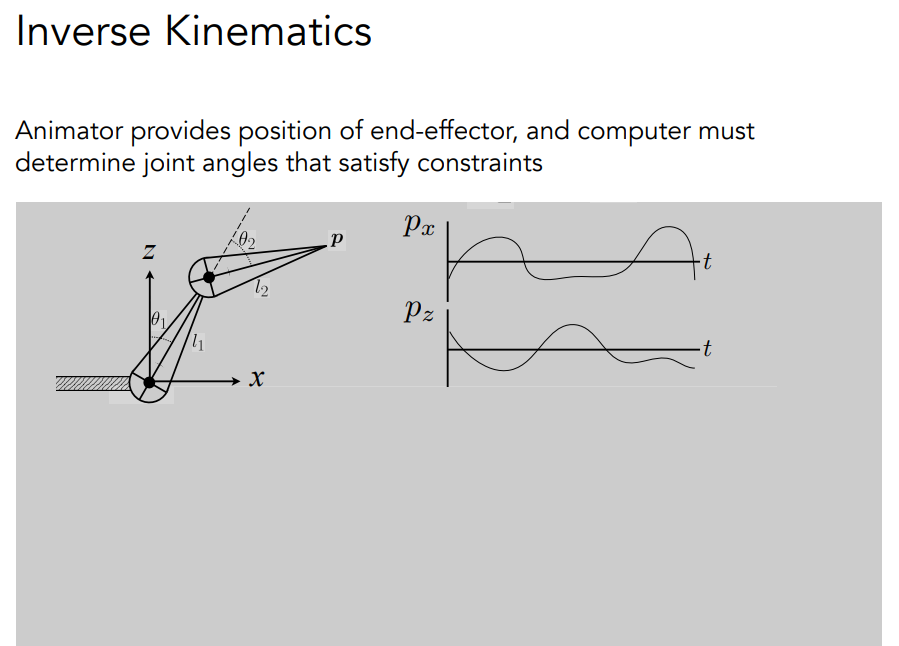
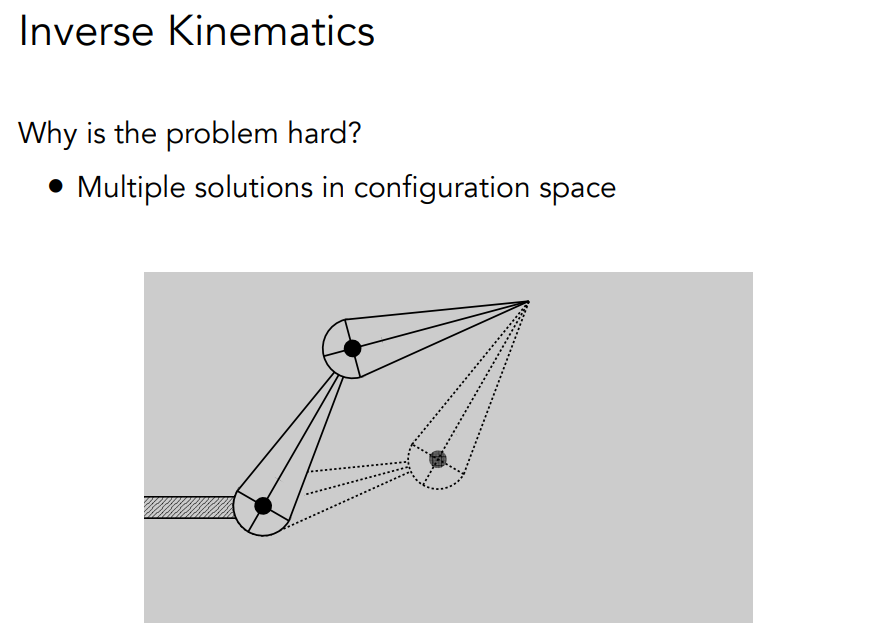
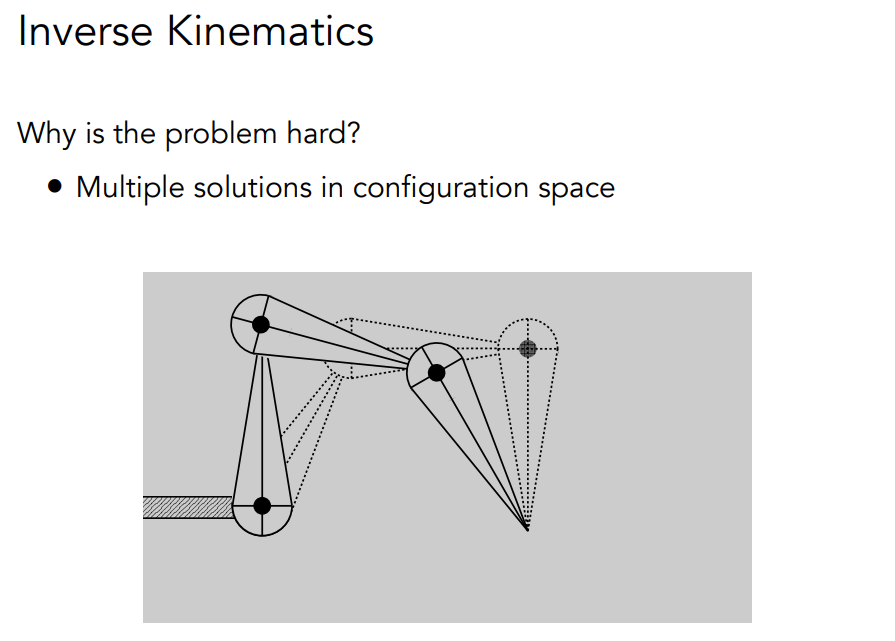
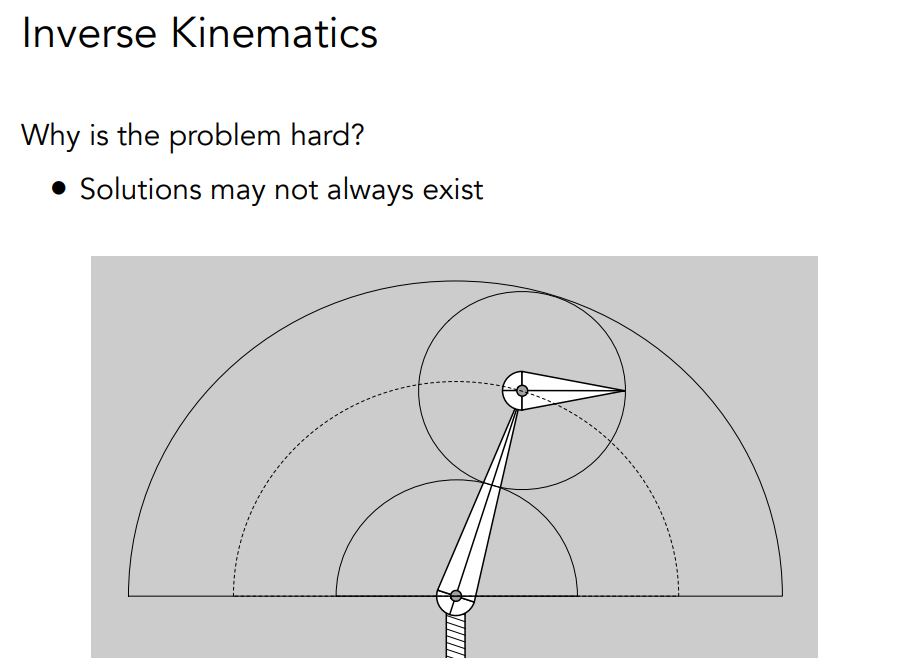
# Inverse Kinematics


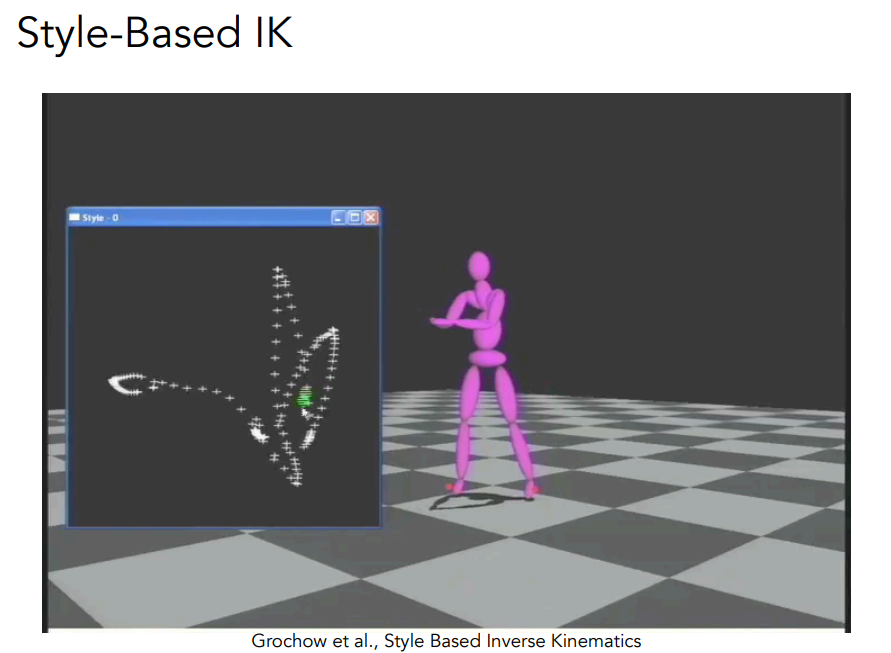
# Rigging




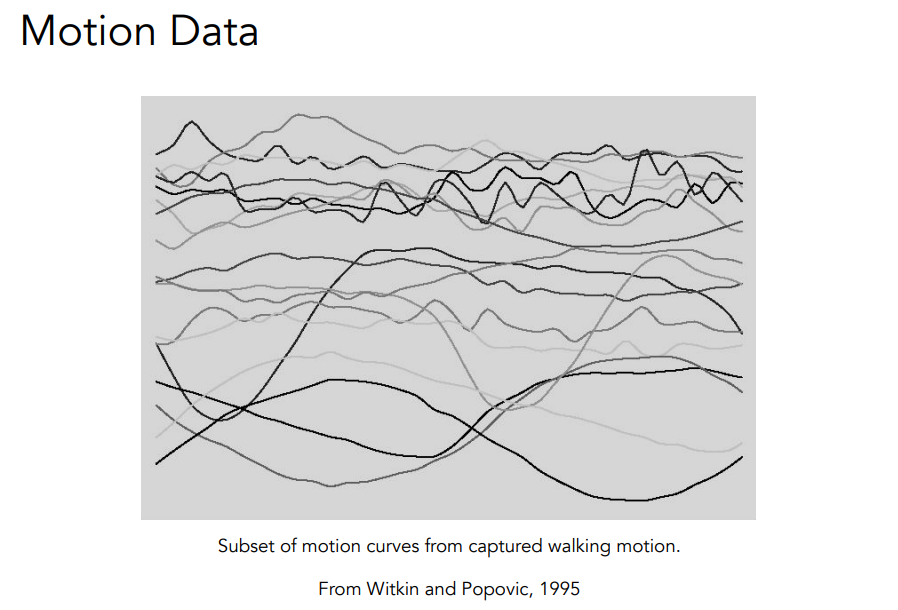
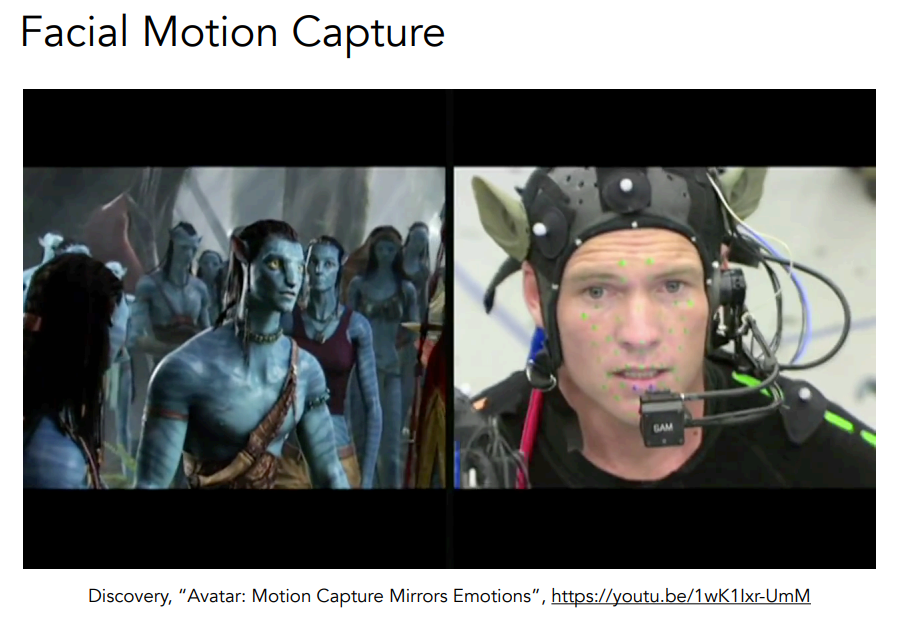
# Motion Capture












# Combating Instability








# Fluid Simulation



