# Cameras, Lenses and Light Fields（相机，透镜和光场）

# Imaging = Synthesis + Capture

我们之前说过计算机图形学里面有两种成像方法，一种是光栅化成像，一种是光线追踪成像，这两种方法都是属于合成（Synthesis）方法，也就是说这些场景本身在自然界中实际不存在。但是我们不止能通过合成方法来成像，还能通过捕捉方法来成像。捕捉（Capture）方法指的是把真实世界存在的场景变成照片，而最简单的捕捉方法就是用相机来捕捉。

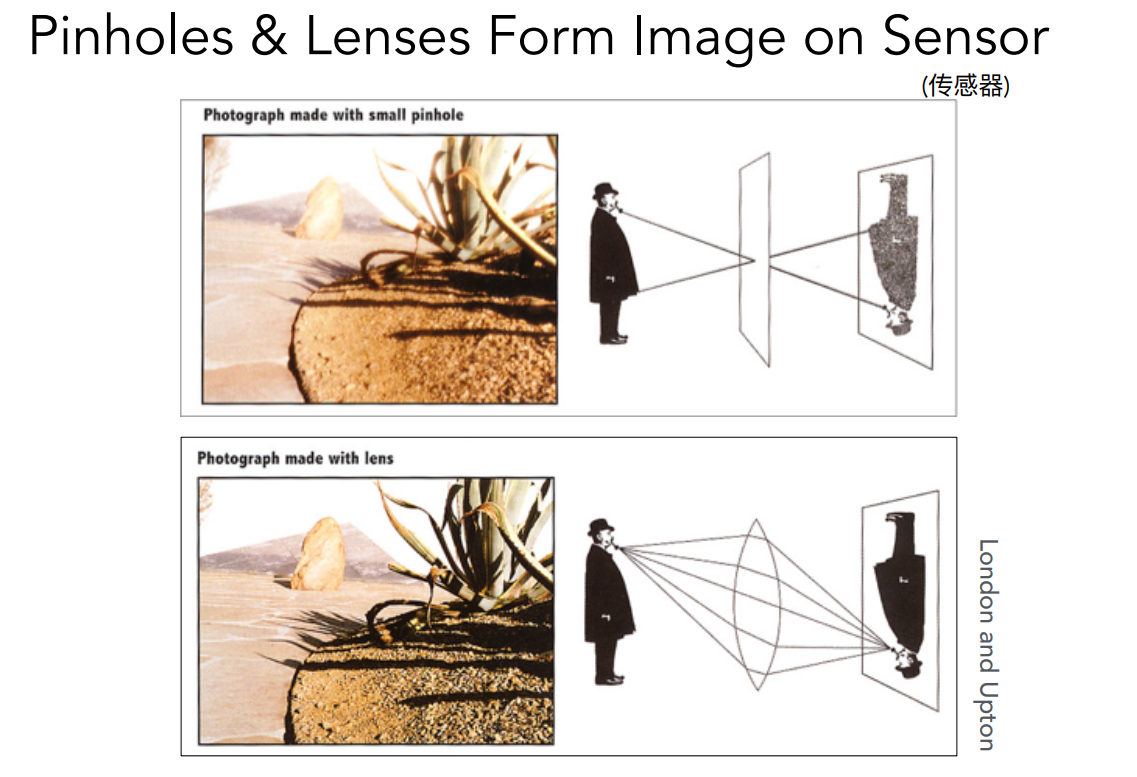
最早的时候大家研究相机是从小孔成像的现象开始的，光线由于直线传播在穿过小孔后会形成一个倒立的像，右边如果再放上一个传感器将其记录在胶片上就能得到一张相片，这种相机也叫做针孔相机。我们平常见的更多的还是上图下面那种带透镜的相机。

上图是一个去掉了镜头的相机，我们看到的这个部分就是控制光是否能够进入机身的一个部件，也就是快门（Shutter）。

当光进入相机之后，还需要一个部件把光捕捉并且记录下来，这个部件叫作传感器（Sensor）。传感器上的任意一个点记录的是 Irradiance 的信息。

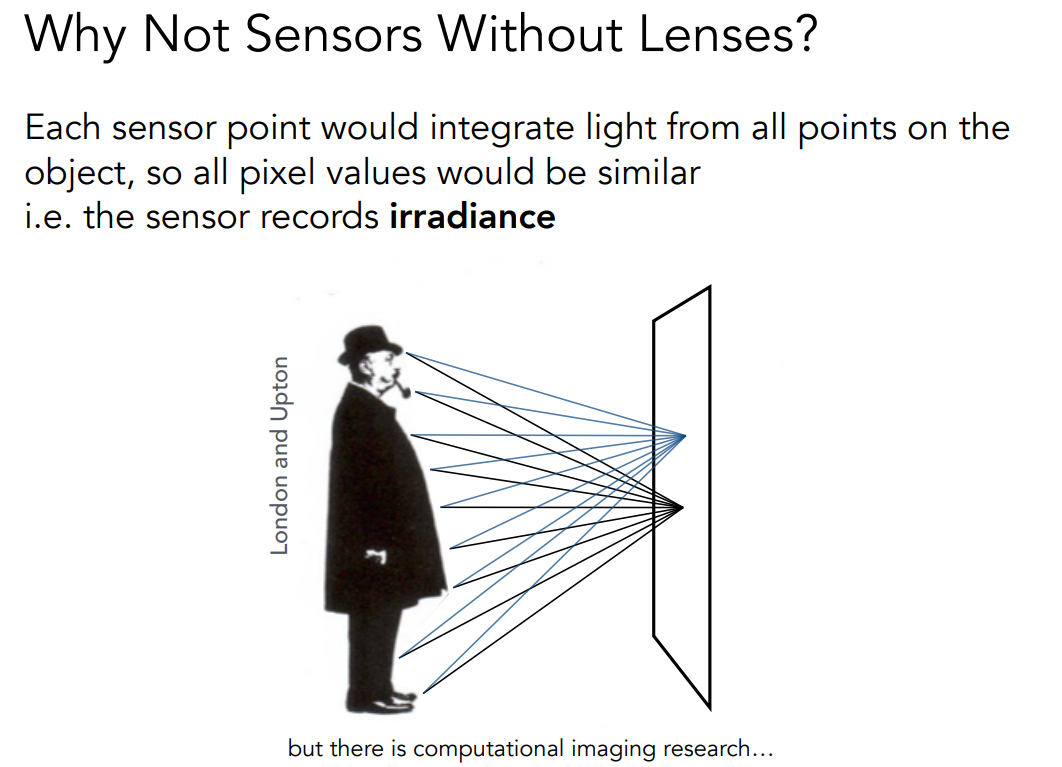
如果一个相机没有镜头，那么它要想拍照是不可能的，这是因为如果直接把传感器放在人的面前，那么传感器的任何一个点都可能会收集到来不同方向的光，也就是说它收集的是 Irradiance 的信息而不是 Radiance 的信息，这样拍出来的东西都是糊的。

# Pinhole Image Formation

针孔相机拍出来的东西是没有深度可言的，也就是说它的任意一个部分都不会是虚的，都一定是清楚锐利的，不会有虚化的现象。我们做光线追踪时用的就是针孔摄像机的模型，因此我们也得不出不同的地方有不同的模糊，所谓景深的效果。

# Field of View (FOV)

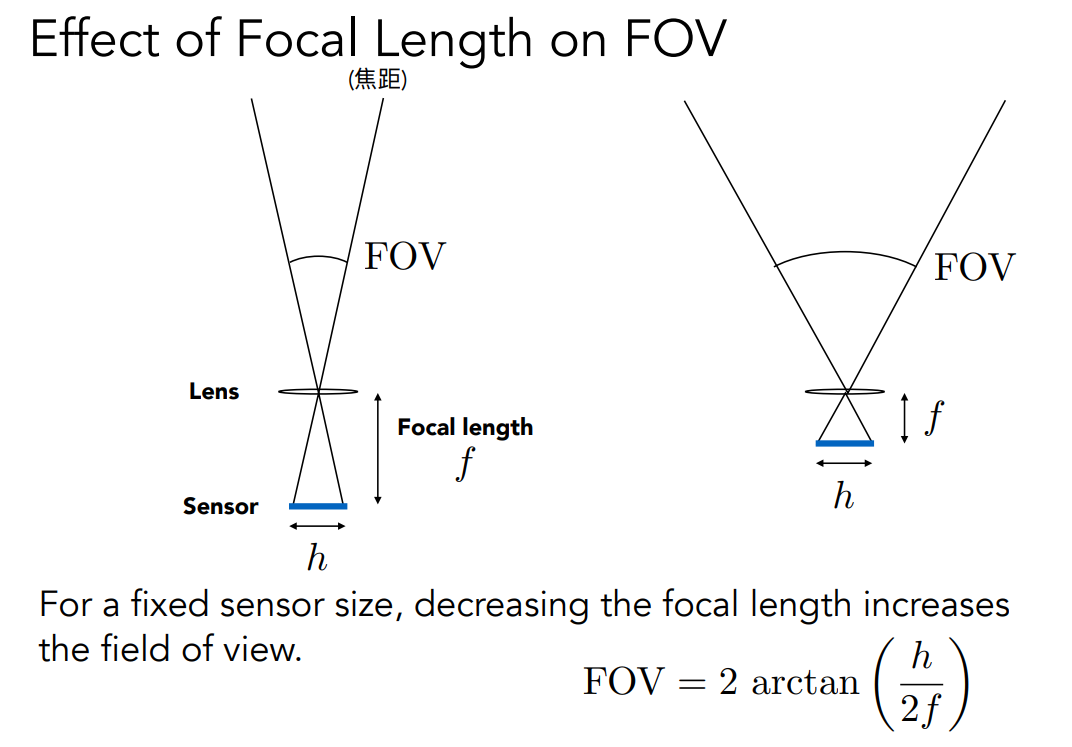
视场（FOV）指的是我们能看到多大的范围，对于广角镜头来说能看到的 FOV 更大，而对于普通的手机来说它们的 FOV 就更窄。我们这里关心的是什么因素能够决定这个视场。从小孔成像的针孔摄像机来理解，我们认为传感器能感受到所有的光线，传感器的宽度为 h，距离小孔的距离叫作焦距$f$，那么 FOV 对应的角度就能通过 arctan 算出来。

不同的视场一定会导致不同的拍照结果，因此我们需要一个严格的定义。由于视场和传感器大小和焦距都有关系，因此人们在定义视场的时候通常以 35mm 的胶片为基准。

不同 FOV 的镜头自然就会拍出各种各样不同的效果，当视场越窄时，我们能看到的地方就越远。

如果我们真的能够改变传感器的大小，那么在相同的焦距情况下，小一点的传感器自然就会对应小一点的视场。这里我们实际混淆的使用了两个概念，一个是传感器，一个是胶片。正常情况下，我们不区分这两个概念没什么关系，但对于渲染来说，传感器负责记录每个像素收到的 Irradiance 有多大，最后用胶片来把它存成相应的格式，因此这两个概念可以不一样，但对于我们目前来说把它们混淆使用也无所谓。

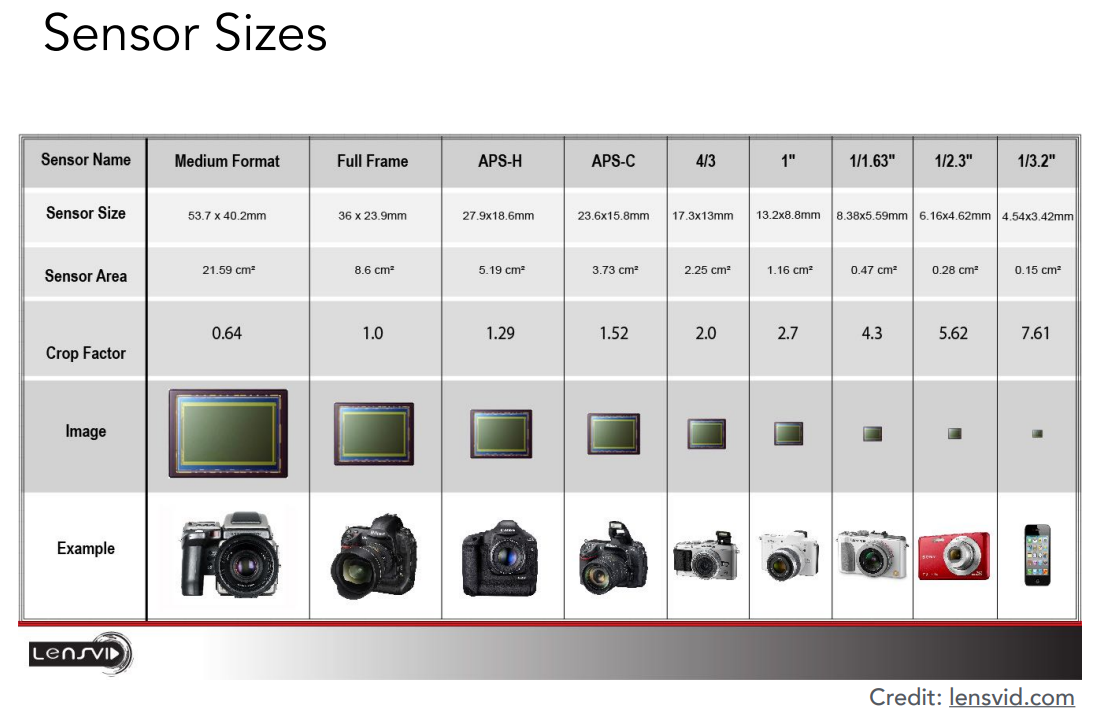
传感器当然可以有不同的大小，对于一个大的相机它就有更大的传感器，也就意味着它有更大的分辨率，因此不同的相机它们的价格各不相同。

如果我们想要让较小传感器的手机拥有和相机相同的 FOV，那么我们就让手机的焦距也给变小，以此就可以达到相同的 FOV。

# Exposure

曝光被定义成 Irradiance 和时间的乘积。如果对着一个明亮的场景拍一张照，那么得到的结果看上去就亮一些；如果对着一个相对比较暗的场景拍一张照，但是快门按下的时间很长，也就是说曝光的时间很长，那么也能得到一个比较亮的照片。也就是说，一个是单位时间进来多少光，一个是进来多长的时间，把这两个乘积起来就能得到曝光度。Irradiance 的大小由很多因素决定，其中一个因素就是光圈的大小，光圈的大小会影响到镜头到底能接受到多少光，也就是说，相机上有很多可以控制的部分来影响最后的曝光度是多少。

那么在相机里面到底有哪些因素在影响最后的照片拍出来亮不亮呢？第一，光圈的大小。由于相机是一个精密仪器，它是可以控制光圈的大小的，这通过 f-stop 来控制。光圈实际上是一个仿生学的设计，对于光圈来说它是在仿照人的瞳孔，人的瞳孔是可以动态调节大小的，如果在相对暗的环境下，瞳孔会自动放大，这样单位时间下就能接受更多的光，能看清更多的东西。如果在相对亮的环境下，瞳孔会自动缩小，以此来防止更多的光进来灼伤视网膜。第二，快门的速度。Shutter speed 越快就意味着快门开放的时间越短，就意味着只能有更少的光才能进来，反之亦然。第三，ISO 增益（感光度）。简单的理解，ISO 是一种后期的处理，当最后感光元件已经感知到了某个层级的光，在后期再给它乘上某一个数来对结果进行修正。

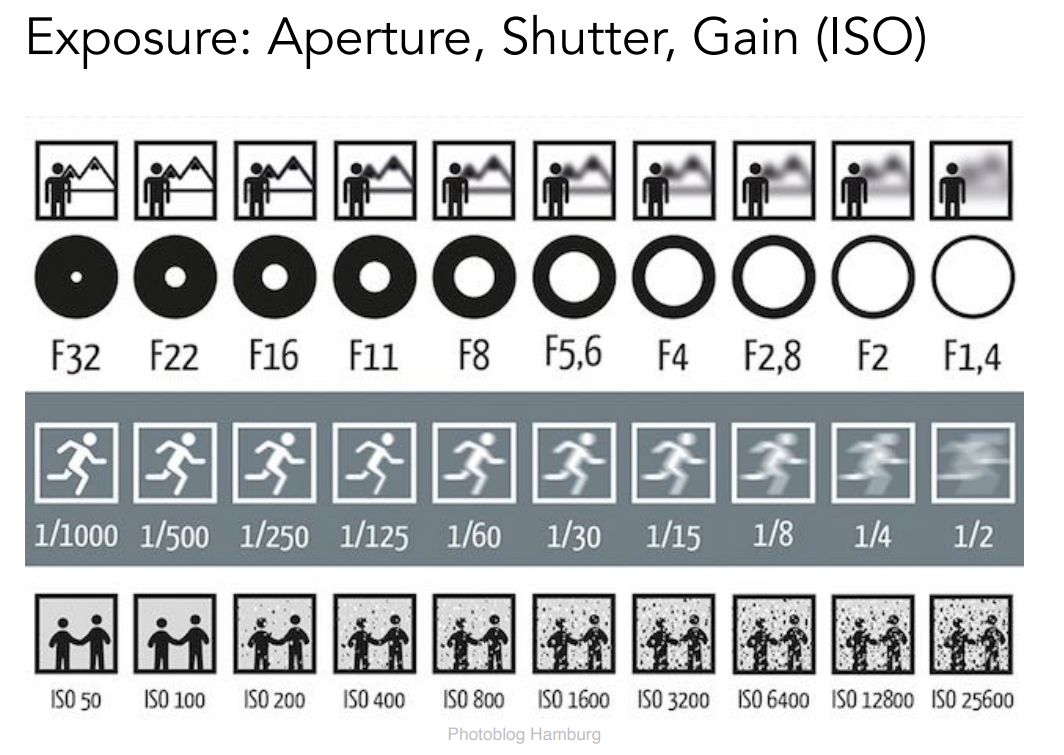
上面这幅图就说明了相机上用各种不同的配置所能得到的结果。例如改变光圈的大小，这里用到了 f-stop 来表示光圈的大小，对应白色的部分，F 数越大光圈越小。Shutter speed 用一个分数表示，意味着快门开放多长的时间，1/1000 意味着开放 1ms。ISO 也能做出调整，不同的 ISO 可以理解为根据大小线性的相乘。另外，我们会发现，当光圈越大的时候，在照片的一定区域就会显得很虚；当快门开放时间越长的时候，会看到动态模糊的效果；ISO 增益越大的时候，由于存在噪声，在放大信号的同时也放大了噪声，因此当在很暗的一个房间里面用很小的光圈，但很短的快门时间，并且用一个相当大 ISO 试图把照片变得更亮，但是结果也会变得更加的 noisy。也就是说对于 ISO 来说，正常情况下不会通过调整它来得到更亮的图，在一定的小范围没有什么问题，在调整非常大的情况下，一定会出现噪声问题。这正是因为简单放大信号会同时放大噪声的原因。为什么会有噪声？这个问题实际上很深刻，这里最简单的一个理解就是把光认为是光子，如果快门时间不够，那么进入到感光元件的光子数就少，光子数那么最后看到的结果自然就很 noisy。

ISO 又叫增益，我们之前也说过，它是在结果上做简单的线性相乘。

我们控制其他的变量，让一张图得到的结果一张比一张暗，然后再通过 ISO 把它们调回来，使它们的亮度相同。我们就会看到，ISO 12800 的图明显比 ISO 100 的噪声明显，也就是说，ISO 确实能够提升曝光度，但是同样会造成噪声的放大问题。

用来描述光圈的大小是有一个数的，我们之前说过叫作 F 数（F-Number，也叫 F-Stop）。F 数有两种写法，一种是 FN，一种是 F/N（N 表示数字大小）。对 F 数的非正规理解是，F 数是光圈直径的逆，也就是 N 越大代表光圈的直径越小。由于光圈影响了在一个时间段内进入到相机内的能量大小，那么调整光圈自然就能得到各种不同的曝光度。

快门一开始是关闭的，之后会突然一下打开，然后再把它关上。这里快门从完全关闭状态到完全打开是有一个过程的，由于有这个过程存在所以会对图片造成一些影响，我们后面再说。

快门的曝光时间当然可以起到调整曝光度的作用，但是除了这个作用，我们还能看到运动模糊的现象。对于高速运动物体就很容易出现运动模糊，这是由于在快门打开的这段时间内，这个物体已经发生了一些运动，由于物体的起止位置不同，但是中间运动的过程也被记录了下来，并且传感器又起到了平均的作用，所以我们就能看到运动模糊的现象。如果把快门的曝光时间延长，那么进来的光就会更多，如果物体以相同的速率运动，那么移动的距离就会更大，那么运动模糊的现象就会更严重。这就反映了为什么用更长的曝光时间会造成更严重的运动模糊，反过来想，如果我们用等长的快门时间，那么物体运动更快就越容易出现运动模糊。我们这里说的快门都是机械式的快门，一些其他方式控制的快门我们这里不做介绍。

运动模糊并不一定是坏事，人们长久以来在感知这个世界的过程中，自然而然产生了有运动模糊的物体运动速度一定是快的这种认知。如果我们不想要运动模糊，那又意味着什么？我们在不同的帧去记录物体运动时不同的位置，由于实际上物体运动是连续的，也就相当于我们在不同的时间对物体所在的位置进行了采样，这就和我们之前说过的反走样非常像了，只不过这里的采样是在时间上的采样，运动模糊就相当于反走样的效果。

对于机械的快门来说，由于快门打开有一个过程。这如果物体的运动的运动比快门还快或者说速度差不多，那么这种情况下就一定会出问题，这个问题叫作 Rolling shutter 问题。例如上图的螺旋桨，我们就会看到明显的扭曲现象，之所以会扭曲是因为图像上的不同位置有可能记录的是不同时间进来的光。

我们把光圈和快门速度两个一起来考虑。快门时间短，那么照片就会暗，那么我们就要提高光圈的大小，也就是用更小的 F 数。上图的表格由于上下的一些对应，让每一列基本都可以达到相同的曝光度。例如 F-Stop 由 4.0 变为 8.0，也就是直径减小了一半，那么对应光圈的面积就变为了原本的 1/4，那么就应该用 4 倍的曝光时间去补偿照片的亮度。但是这并不意味着这两种方式得到照片的结果是一模一样的，我们之前也提到过大光圈会引起前景深的问题，我们之后还会分析，曝光度还会影响运动模糊。因此这两个参数正常情况下都是需要权衡的。

# Fast and Slow Photography

如果平时经常摄影，我们可以拍出一些非常有意思的照片。高速摄影是每秒钟拍更多的帧数，然后再按照正常的速度来播放。而每一秒要拍出更多的照片，就意味着每一张照片留给它的快门时间就非常的短，但是我们又想让图片有正常的曝光度，那么就需要用更大的光圈或者更大的 ISO。

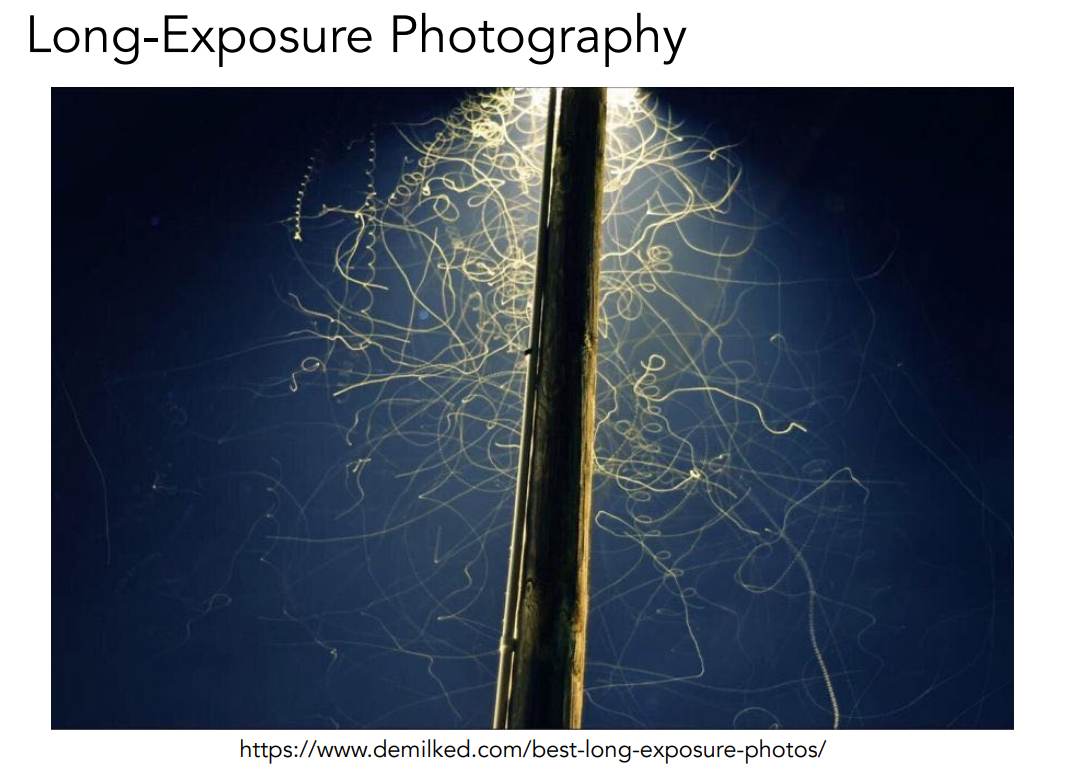
与高速摄影相反，低速摄影就是给照片特别特别长的曝光时间，并且用非常小的光圈去拍摄，这样拍出来的东西就是延时摄影。上图就是一个飞机着陆时的飞行轨迹。

# Thin Lens Approximation

我们之前一直都在说相机各种不同地方的部件，还有一个最重要的部件我们还没有讲，那就是镜头。对于真正的摄影设备来说，它们的镜头都非常复杂，因为它们都会用透镜组来完成成像。

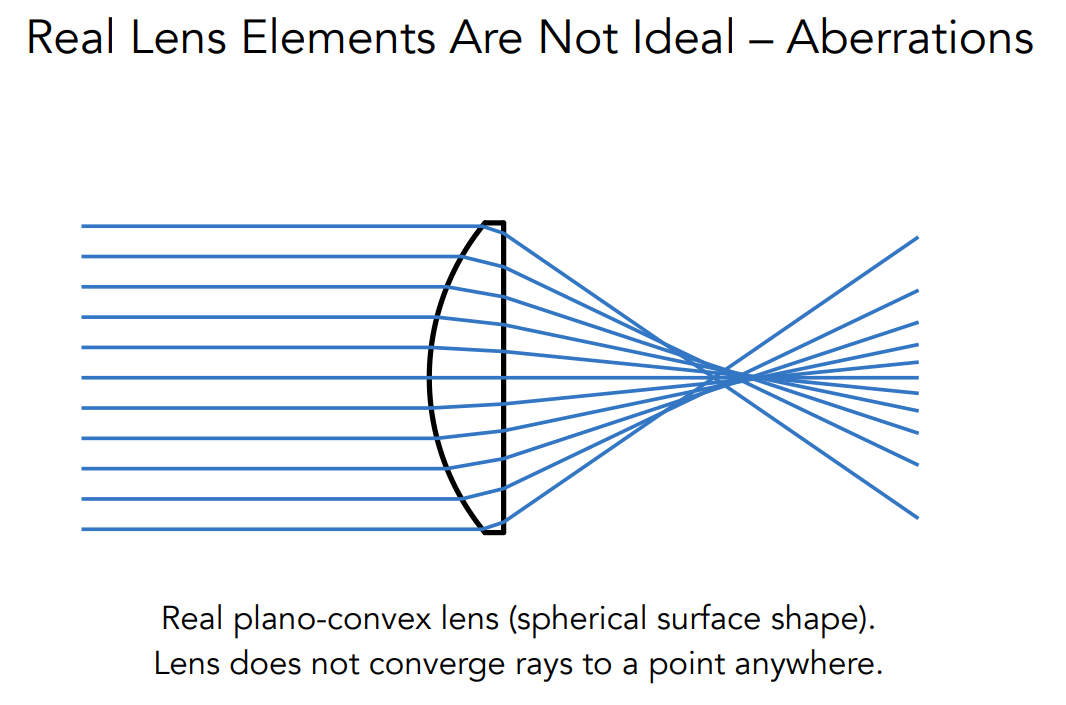
有一些透镜还不像我们通常假设的那种，它一面是凸的，一面是平的。像这种透镜它就不可能把光聚集到一块儿去，从而出现了 Aberration 这种性质。也就是说，实际的透镜可能很复杂，我们这里做了简化处理，也就是理想化的薄透镜，即透镜的厚度不作考虑。

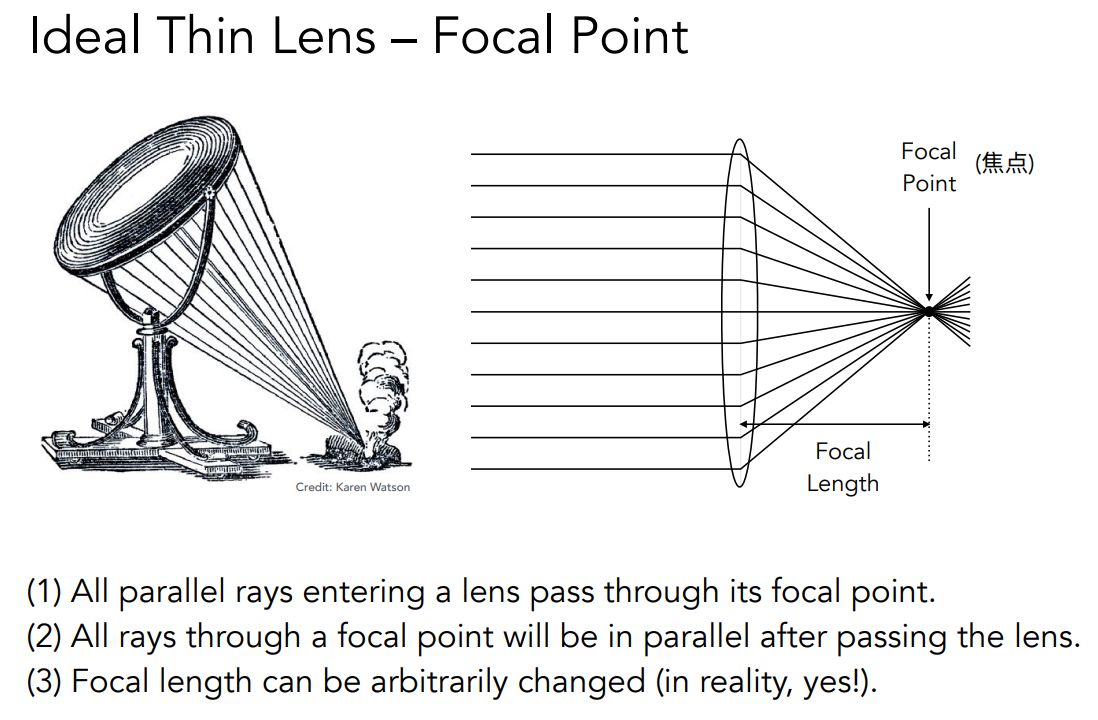
理想化的情况，对于一束穿过透镜的平行光，它们都会被集中到一个点上，这个点叫作焦点，那么焦距就是焦点到棱镜中心的距离。由于光路有可逆性，也就意味着如果光线穿过了焦点被透镜折射之后就会变成平行光。我们这里还会假设这个薄透镜可以任意地改变它的焦距。虽然对于一个设计出来的透镜来说，它的焦距一定是固定的，我们之所以认为它能改是因为相机的透镜组通过不同的组合使得就好像是一个薄透镜能够任意的改变它的焦距一样。

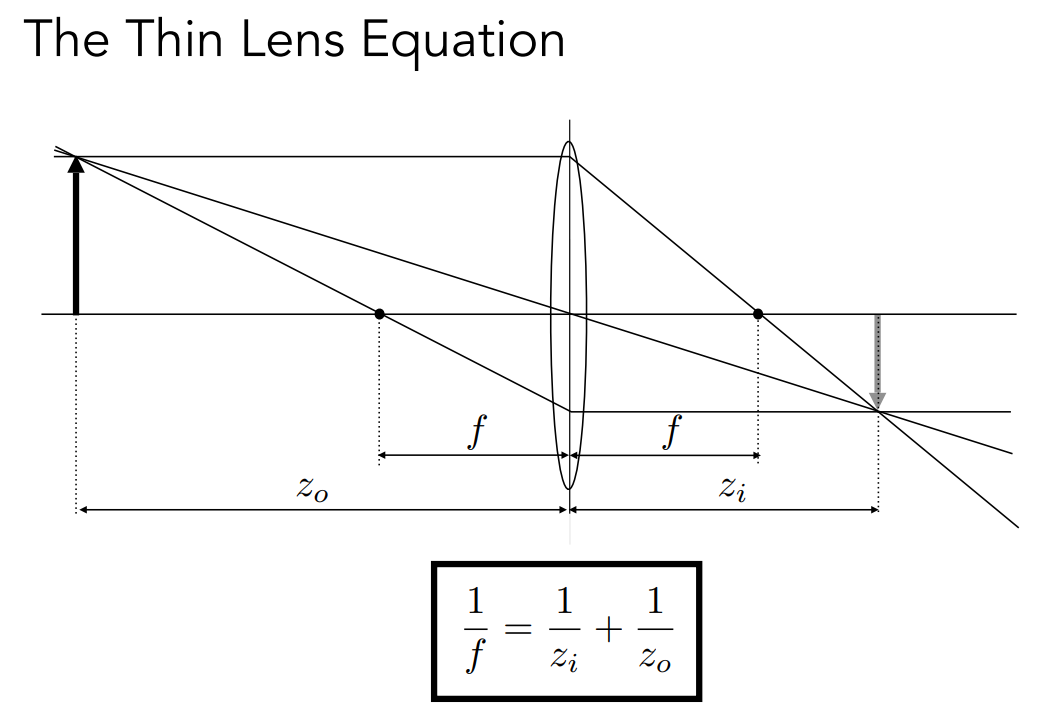
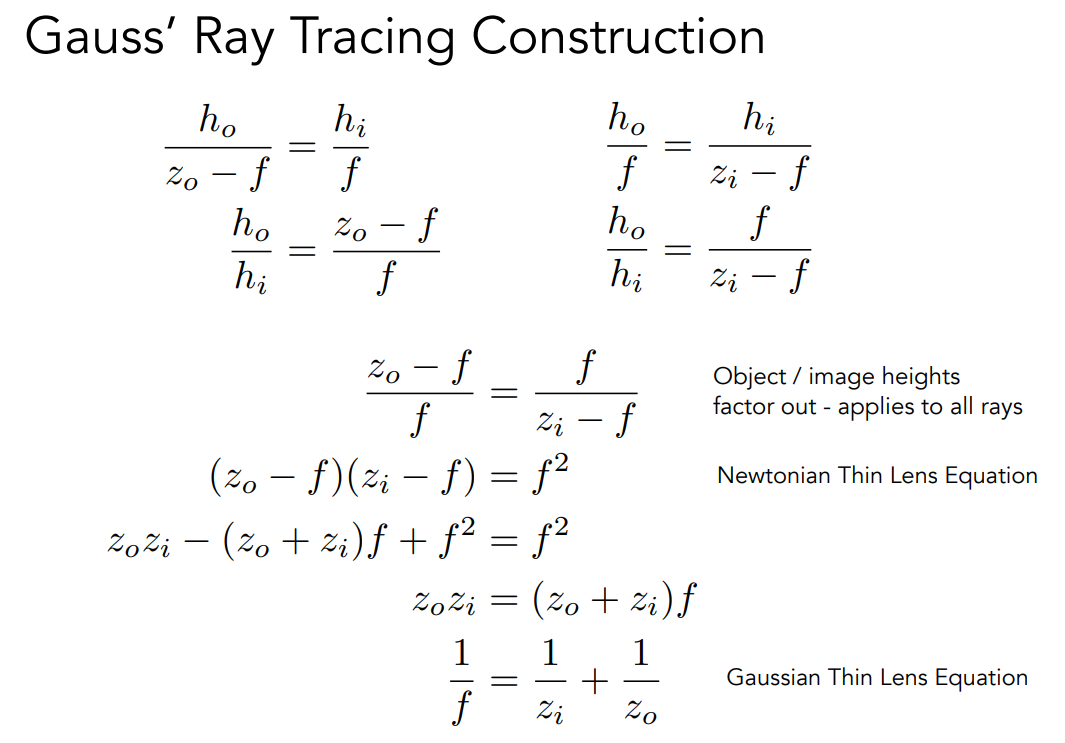
透镜会满足一些基本的物理规律。除了我们之前说的平行光过透镜会被聚焦到焦点，以及过焦点的光会变成平行光出去之外，我们还会认为穿过透镜中心的光线它的方向不会发生改变。上图我们定义了物距$z_o$、像距$z_i$，以及透镜的焦距$f$。那么它们之间会满足上面的一个式子。这个式子说明对于一个固定焦距的透镜来说，如果改变它的物距，那么它的像距也一定会跟着改变。

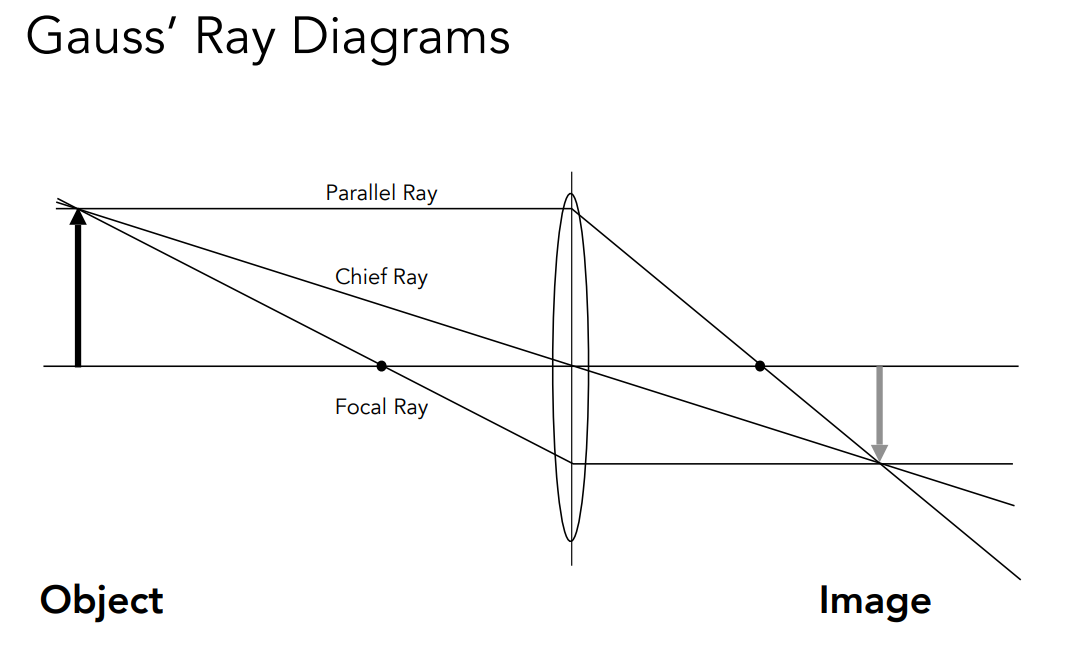
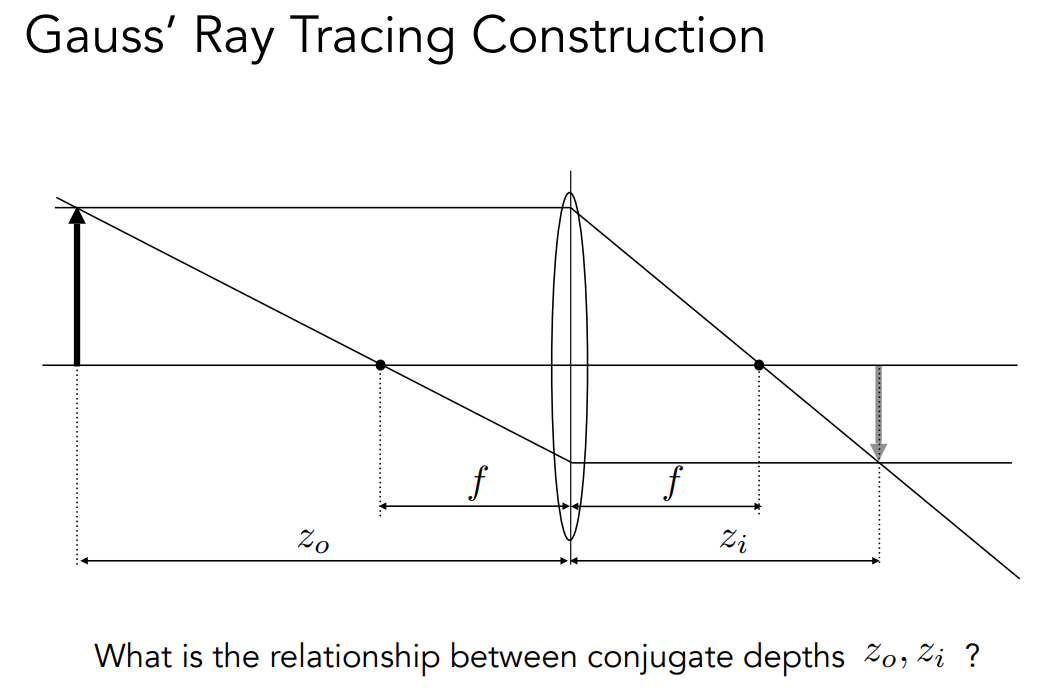
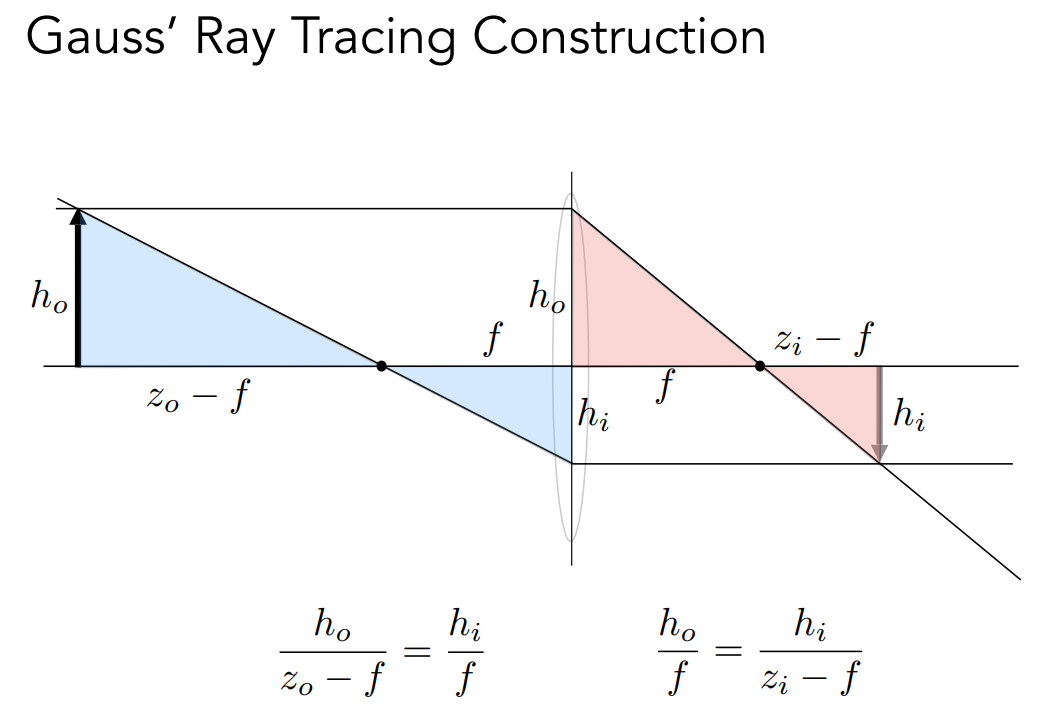
# Defocus Blur

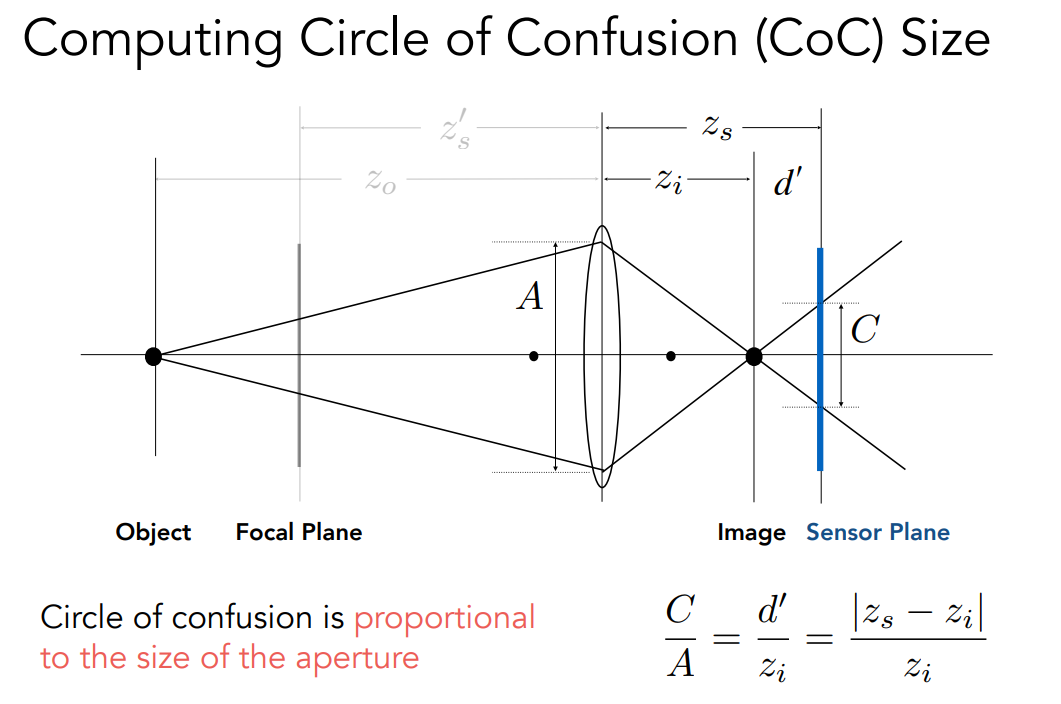
通过薄透镜我们就能就是很多很多的问题，我们先来看看 Defocus Blur（散焦模糊），这也是涉及到景深的一个问题。为了解释模糊，我们需要引入一个概念，叫作 Circle of Confusion（CoC）。原本我们知道远处有一个平面（Focal Plane），这个平面上所有的光经过透镜之后都会被聚焦到右边成像的平面上（Sensor Plane），如果说有物体不在 Focal Plane 上，那么这个物体看上去就会比较模糊，这是由于根据之前得到的焦距、物距以及像距之间的关系，我们知道了 Object 会成像在 Image 这个平面，但是我们的成像平面（Sensor Plane）并不在这个地方，因此光线没有发生碰撞会继续传播，这就意味者左边一个点经过透镜被感光元件接收到的时候，它就不再是一个点了，而成了一个圆，这个圆就叫做 CoC。通过相似三角形我们可以写出上面的式子。假如$|z_s-z_i|\over{z_i}$ 为定值，那么相机拍摄某个物体的模糊程度是和 aperture 的大小成正比的。

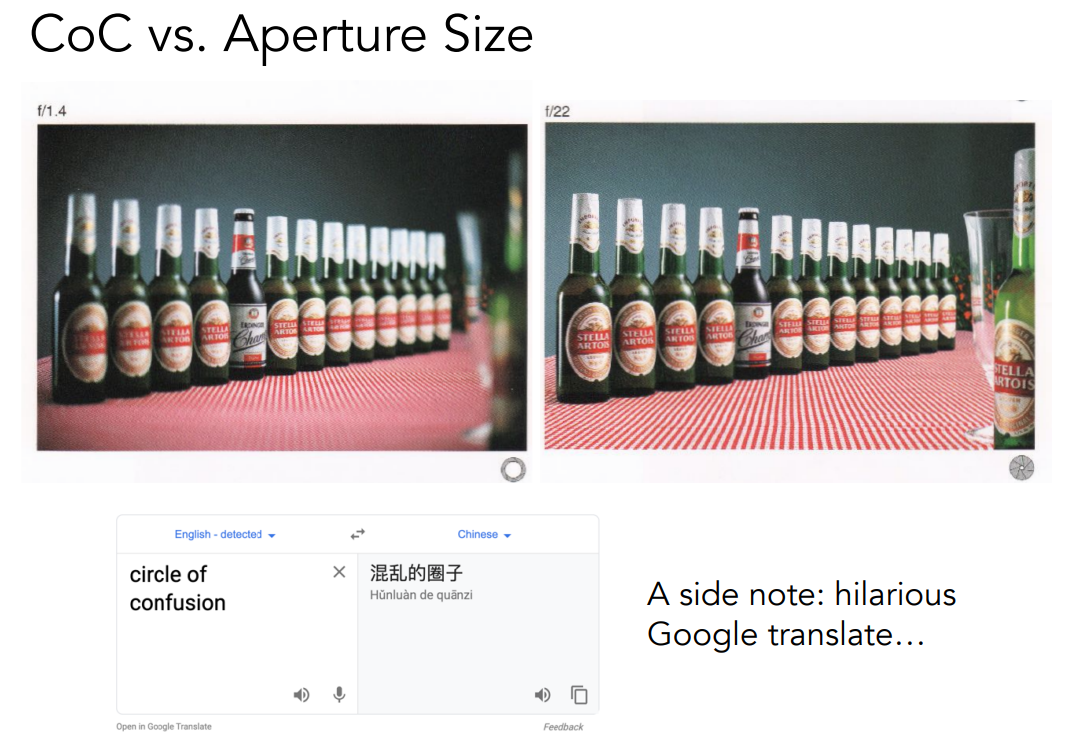
CoC 告诉了我们看到的东西模糊不模糊取决于光圈的大小。

既然说 CoC 和光圈的大小成正比，我们现在来给光圈一个正式的定义。之前我们简单的把 F 数定义为光圈直径大小的逆，这实际上是不对的，F 数实际的定义是焦距除以光圈的直径。

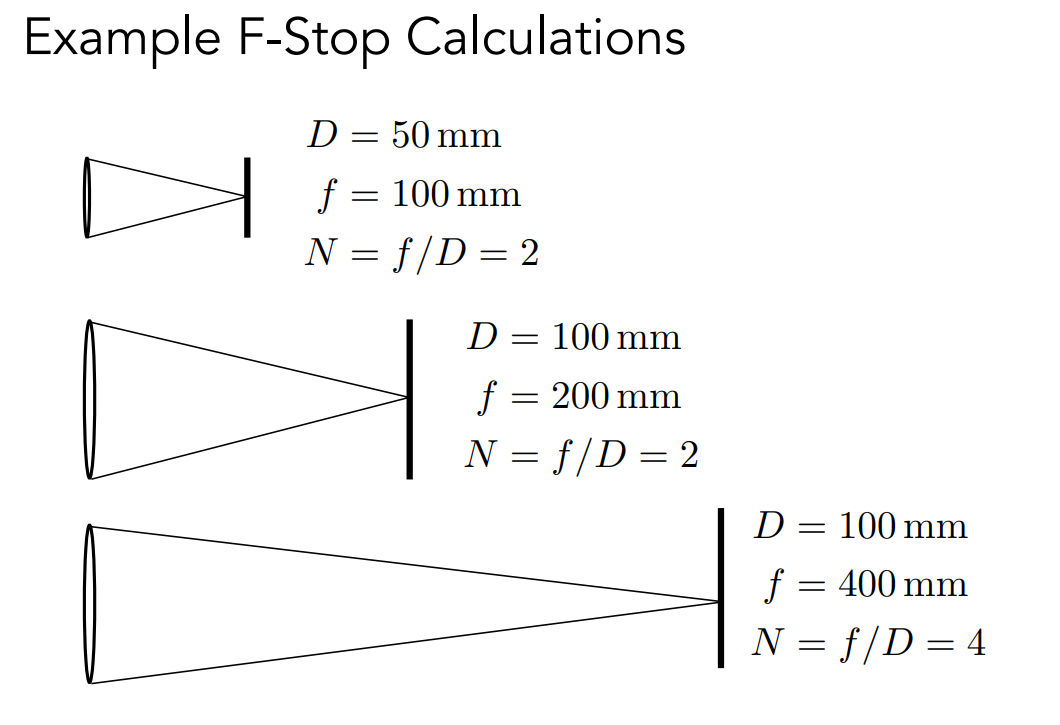
知道了$A=f/N$ 之后，我们又可以看出来 CoC 和 N 是有反比关系的，也就是说平时我们为了拍出更清楚的照片，那么就要用小光圈。

# Ray Tracing Ideal Thin Lenses

我们现在已经知道光线会怎么穿过薄透镜，那么自然而然我们就可以使用薄透镜来渲染。之前做 Path Tracing 的时候，我们都是从相机往任何一个像素中的采样点去连线，其实就默认了这是小孔成像的模型，即针孔摄像机的模型。但是我们完全可以模拟出一个薄透镜的渲染过程。

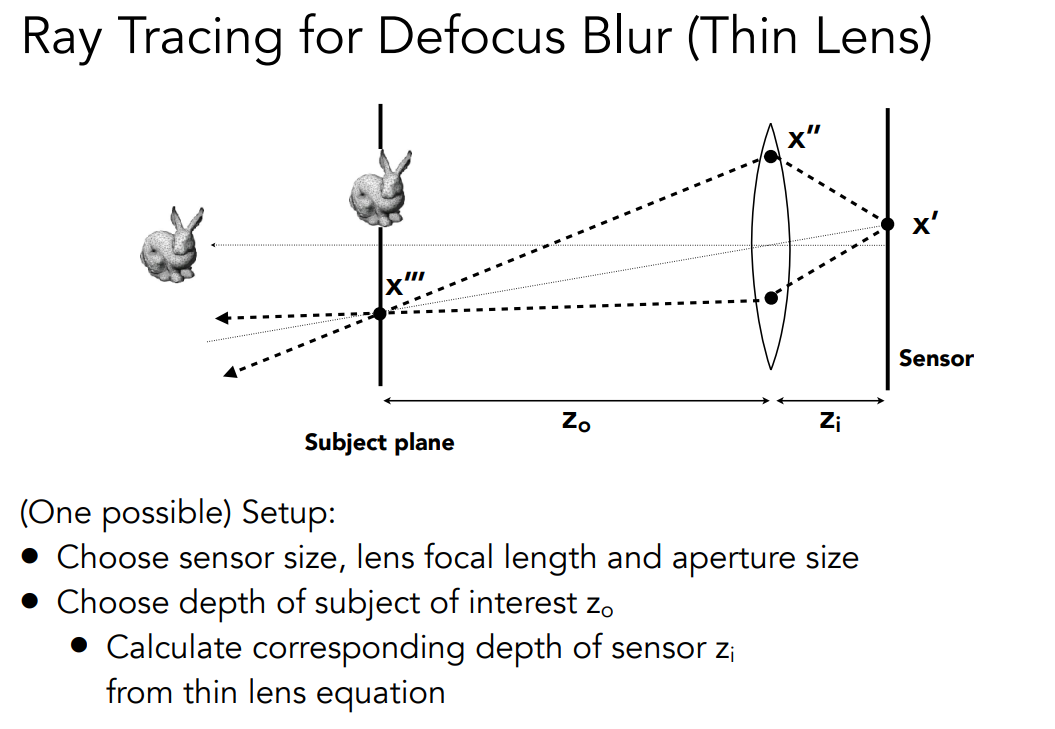
在上面的场景中，我们确定了传感器的大小、透镜的焦距和光圈的大小。并且把透镜到我们想要拍摄的平面（Subject Plane）之间的距离记为$z_0$。现在，透镜的属性设置好了，传感器也设置好了，并且它们都被放到场景中指定的位置上了，那么根据薄透镜公式，我们就可以求出传感器和透镜的距离$z_i$。

接下来就可以开始实际做 Ray Tracing。我们现在就是想找一些光线让它们穿过透镜打到场景里面去，那么就在 Sensor 上面找任意找一个点$x'$，并且在透镜上选另外一个点$x''$，然后把这两个点连一条线，之后我们就能立刻知道这条线经过透镜折射之后打在 Subject Plane 的一点$x'''$ 上。之后我们就能把$x''x'''$ 这条线上的 Radiance 记录到$x'$ 这一点上。

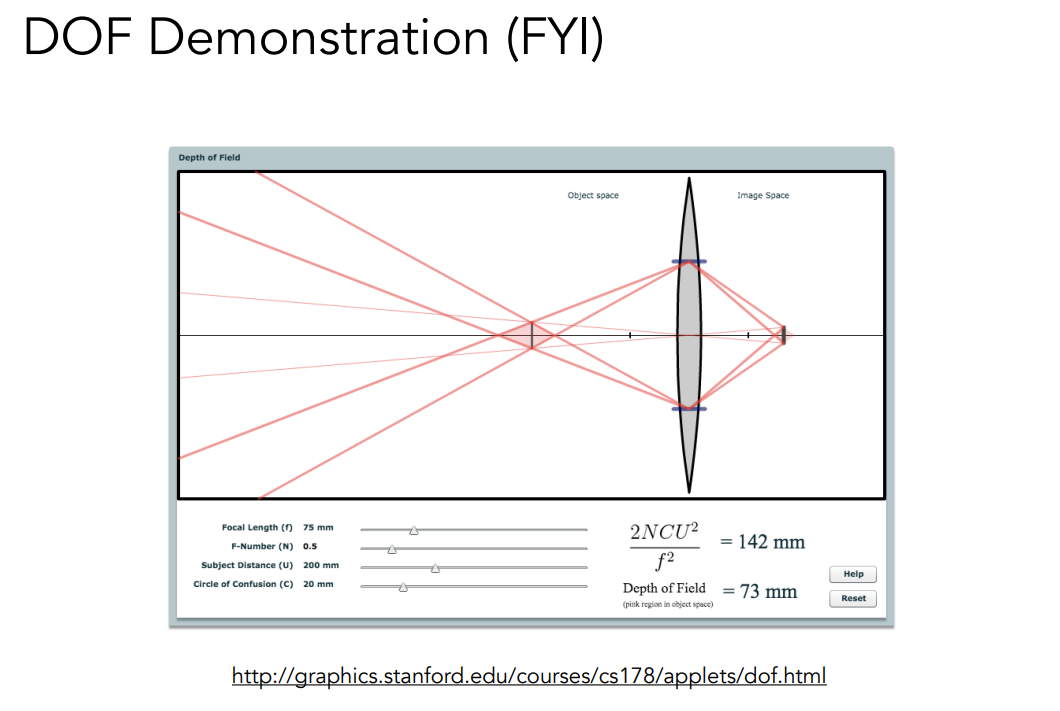
# Depth of Field

接着，我们就可以用 Defocus Blur 来正式的定义景深的概念。上面两张照片就是用不同的光圈大小拍出来的。我们之前说过，大的光圈对应大的 CoC，成像的一个点到传感器上形成了一个大的圆，所以就会更模糊。但是，总归有些地方它是不模糊的，也就是 Focal Plane，在这个平面上都是不模糊的。也就是说，不同的光圈大小会影响到模糊的范围。

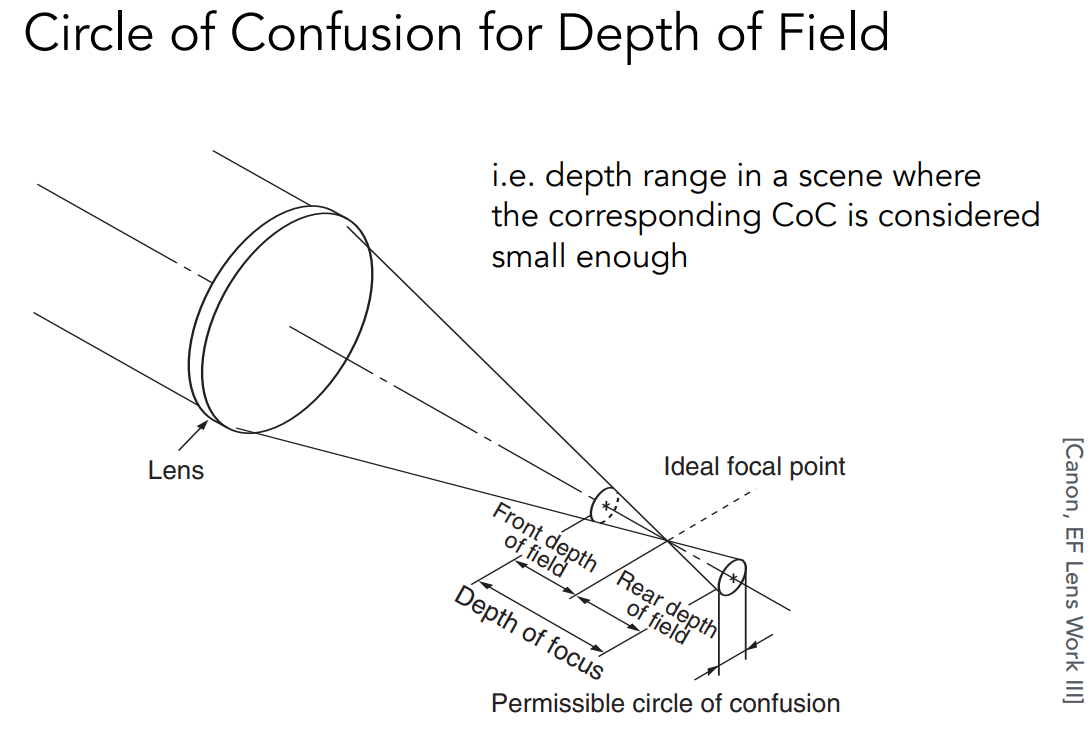
现在有一束光经过透镜它会打到某一个成像平面，在这个成像平面的附近一段区域内我们都认为这个 CoC 是足够小的。而景深就是指，在实际的场景中有一段深度，这段深度经过透镜之后会在成像平面的附近形成一段区域，这段区域内我们认为 CoC 都是足够小的。那么我们想要算景深，其实就是想算在 CoC 很小的一段范围内，我们基本认为对应看到的场景那一段它是清晰的。之所以可以这么理解，是因为成像平面由像素构成，每个像素都是有大小的，当 CoC 的大小跟像素相比差不多或者比像素小时，我们都可以认为最后得到的结果是锐利的，这就是为什么我们不止说这个成像平面自己，在成像平面附近一个微小的范围都是可以认为这段成像出来结果都是锐利的。

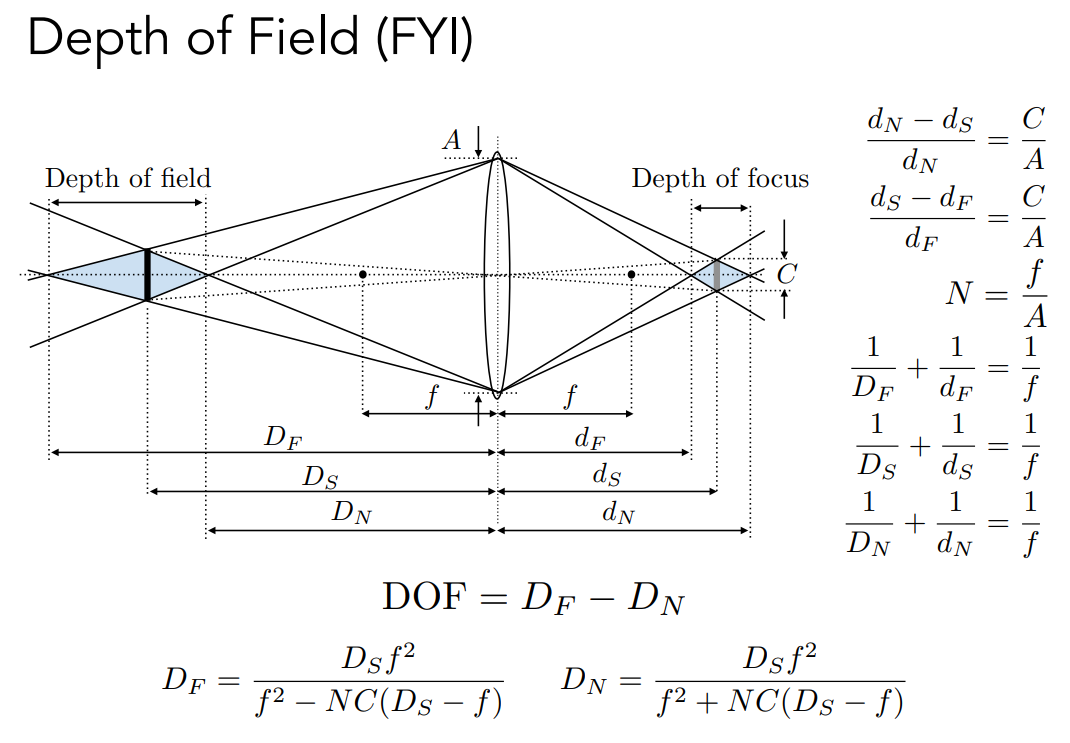
我们可以考虑这个景深的最远处和最近处，并且能得到它们穿过透镜后所形成的一段成像范围，并且我们希望把$D_F$、$D_S$、$D_N$、$d_F$、$d_S$、$d_N$ 和$f$ 联系起来（通过相似三角形和透镜公式）。于是，我们就能把 DOF（景深）给解出来。

# Light Field / Lumigraph（光场）

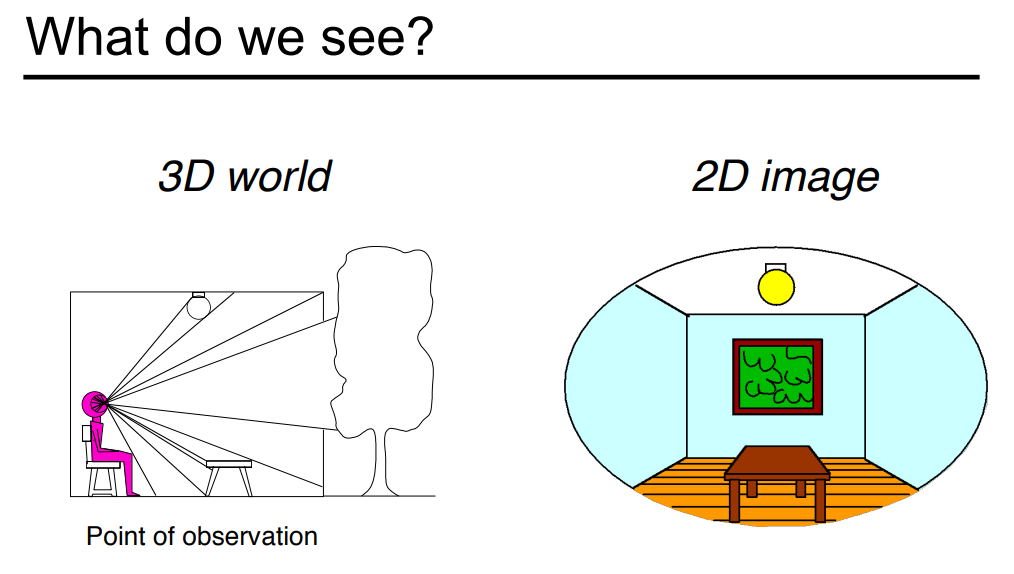
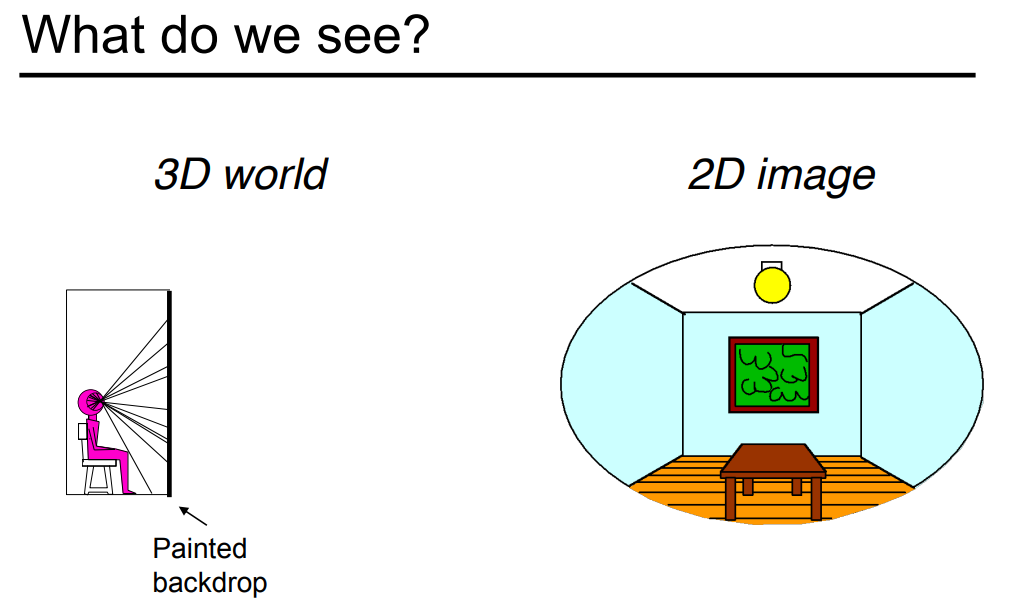
在解释光场之前，我们先从我们看到的世界说起。我们设定一个简单的场景，小人坐在一个凳子上看整个屋子，并且透过窗户可以看到一棵树。如果我们把他看到的东西画下来，那么就是一张图。如果我们在房间的中间加上一层幕布，这个幕布能够严格意义上模拟小人之前看到光线从某一个点打到另外一个点的强度是多少。这个幕布我们就让它显示我们之前所能看到的这张图，那么小人坐在那里看那张幕布是绝对体会不到这块幕布和真实世界有区别的，这也是虚拟现实的原理。也就是说，只要我们把所有的信息都记录在这样一个平面上，然后考虑这个平面上的任意一个点往任意一个方向发出来的光，如果把这些信息都完整地记录起来然后被人看到，那么是严格意义上和人看到的真实场景是一模一样的。

我们能够描述人到底能够看到什么东西，可以用全光函数来表达。全光函数描述了我们能看到的所有东西。我们从最简单的全光函数开始说起，然后一步一步把它说明白。

假设我们站在一个场景里面位置固定，并且我们可以往四面八方去看，于是我们可以定义任意一个方向（用极坐标表示，$\theta$ 和$\phi$）。那么我们就可以定义$P(\theta,\phi)$ 表示从任意一个方向看能得到什么样的一个值。

我们可以把这个函数再改进一点，我们会引入一个波长的概念。既然是波长，也就说明我们引入了各种各样不同的颜色。如果我们把向任意一个方向上看到的对应波长的光给记录下来，那么就相当于我们看到了一个彩色的世界。

我们再对上面的函数扩展一个时间 t，那么我们就能看到电影。因为我们能往各个不同的方向看并且这个信息是彩色的，然后在不同的时间看到的东西还不一样。

再进一步扩展，我们可以让人的位置或者摄像机的位置在三维空间中任意的移动。三维空间中的任意一个位置我们知道（X、Y、Z）。既然连各个位置看到的东西都定义了，那么我们看到的就是全息电影。也就是我们不仅能够看到整个世界，还能改变自己的位置从另外一个角度来看这个世界。

我们还可以最后再改进一步。也就是我们不把这个函数当作电影来看，而是理解成在任何位置往任何方向看，并且在任何时间我们看到的不同的颜色，那么这就是我们所看到的所有的事情。整个一个视觉的世界其实就是一个七个维度的世界。到此为止，我们就能把这个七维的函数叫做全光函数，并且所有的整个世界都可以拿这个函数来表示了。

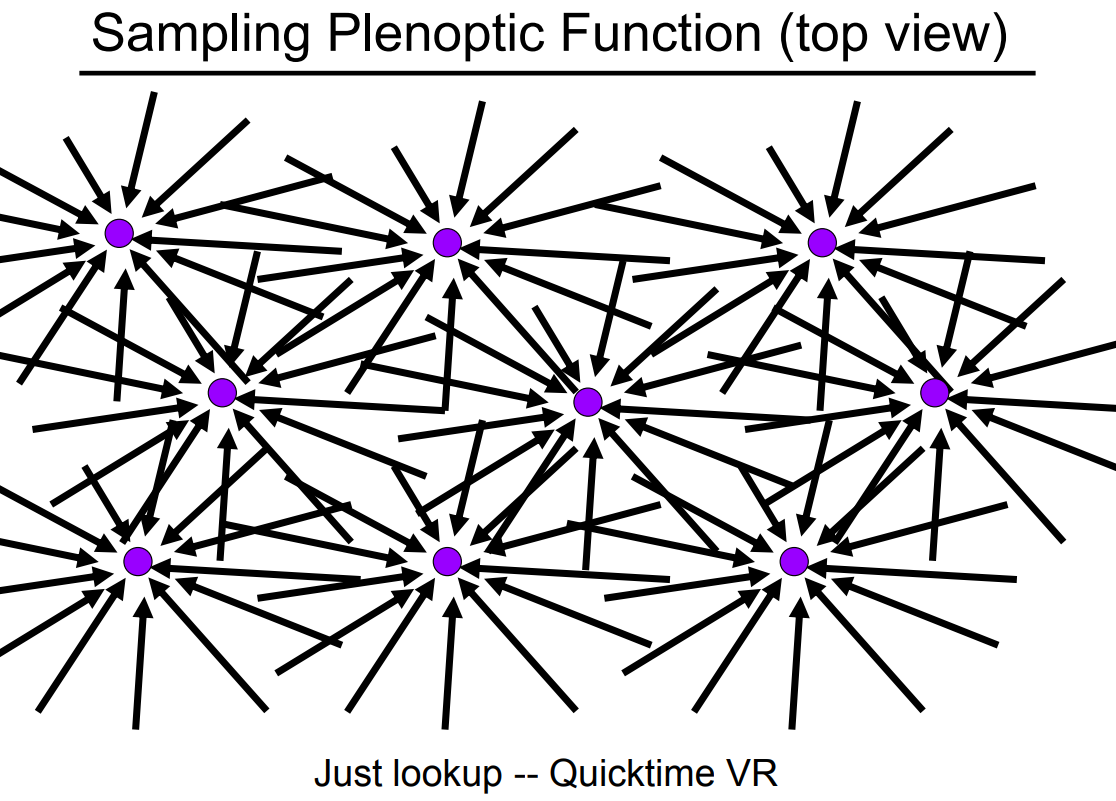
光场的概念就是从上面讲到的全光函数开始的。我们先从全光函数本身的定义上来看，也就是上面紫色的点可以在任意一个位置上，并且从任意一个方向我们都能知道过来的光是多少，并且这些信息都是连续的。也就是说，我们可以从全光函数中提取一部分信息出来，用它们来表示一些更复杂的光，光场实际上就是全光函数的一个小部分。

定义光场之前，我们先来定义光线，三维中的任意一条光线可以用$P(\theta,\phi,V_X,V_Y,V_Z)$ 来表示。

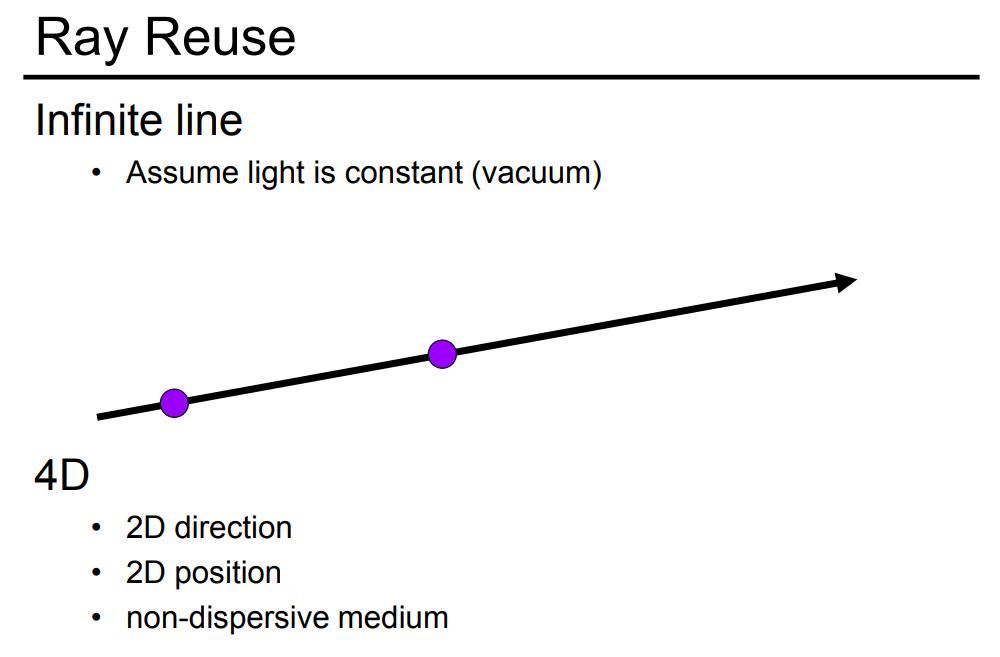
我们会发现上面那个对光线的定义需要一个起点和一个方向，但也不一定说这种方式的定义就是最好的，还有其他各种各样的方式来定义这样一条光线。例如，我们只要知道了光线上的两个点就能定义出一条光线（方向可以通过正负来定义）。这样的话，我们要向定义一条光线就只需要二维的位置和二维的方向。

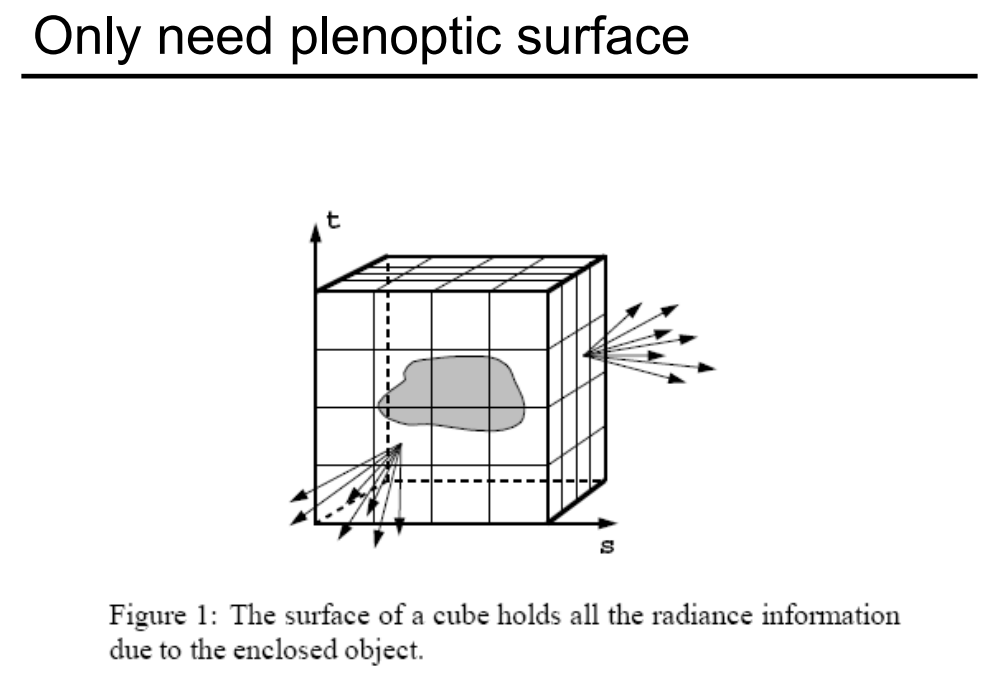
如果我们想定义对于任意一个物体它的表面（这个物体可以被放在某一个包围盒中），那么我们看向这个物体，无非就是从任何位置、任何方向去看向这个物体。反过来，通过光路的可逆性，我们也可以认为要想描述物体所能被看到的所有情况，就描述这个物体在它的包围盒上任意一个位置往任意一个方向上过去的光线，只要把这个过程描述清楚，我们就可以得到从任意一个位置看向这个物体它应该长什么样了。因为我们从任何位置看向这个物体，就相当于包围盒上有一个点并且和观测的位置两点确定了一条光线，并且我们知道它的方向，那么我们就能够查询之前记录的函数。这个函数记录了在物体表面不同位置的点往各个不同的方向的发光情况，如果我们把这个信息记录下来，这就是我们要的光场。总结一下，光场就是在任何一个位置往任何一个方向去的光的强度，这样一来我们就在光场和全光函数之间建立起了联系。光场是全光函数的一小部分，只是二维的位置和二维的方向。现在我们回过头来再来理解二维的位置和二维的方向，3D 世界中，三维物体的表面实际上是在一个二维的空间中的，空间中的方向我们也可以用$\theta$ 和$\phi$ 来表示。也就是两个数来表示方向，两个数来表示位置，这就是光场。

如果我们有了一个物体的光场，物体上的任何一个位置往任何一个方向都可以发光。我们之前说的是，在任何一个位置向物体看过去，只要有光场我们就能知道能看到什么（由于之前记录光场的时候，任何位置往任何方向都记录过光线所带的能量）。有了光场之后我们得出一个结论，我们可以得到各种物体不同的观测。这也是光场的好处，它是一个四维的函数，能给我们任意的一个观测方向所能看到的结果。

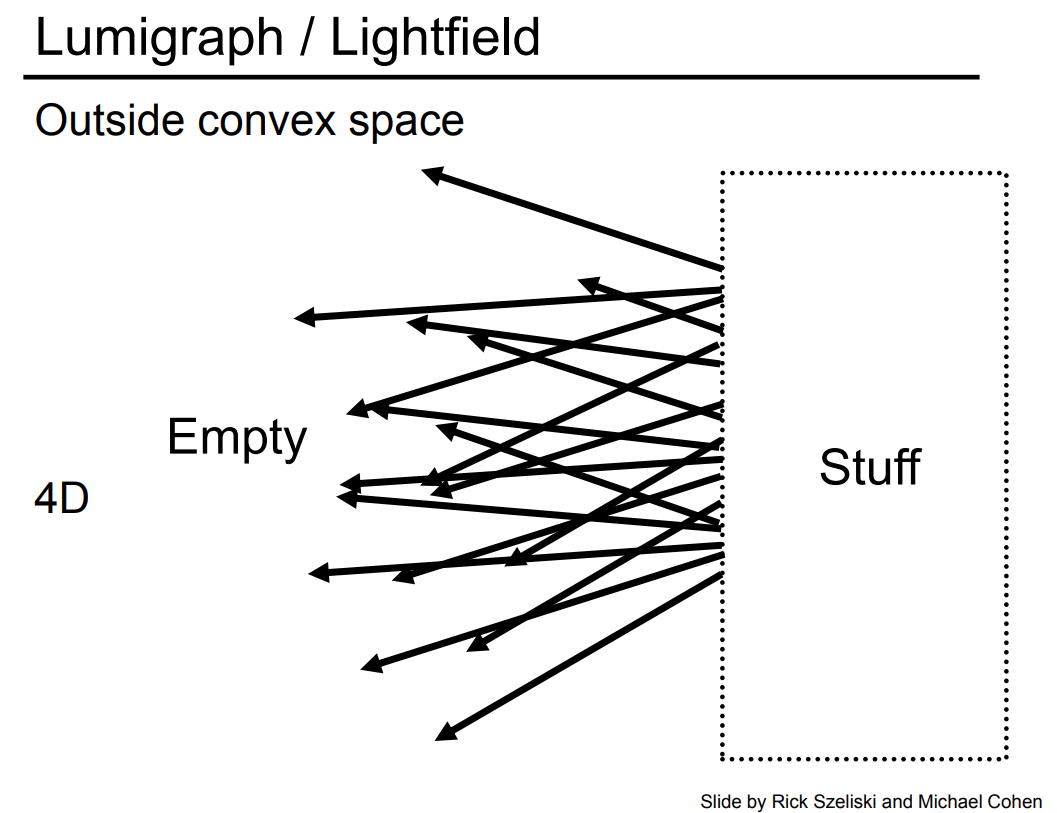
我们之前提到过光场是定义在物体表面的，但是前一个例子我们又说把物体放在一个包围盒里，并且我们不需要知道盒子里的物体是什么，我们只需要把盒子上的任意一个点它往任意一个方向的光给记录下来就可以。也就是说，我们不需要知道光场表示的是个什么东西，而只用把它看成一个黑盒，在盒子的表面的任何一个位置都能知道任何一个方向的光线，这样我们就能记录光场（前提是观测点在包围盒的外面，在里面我们没有记录信息）。

更进一步，这种方式我们还可以理解为取一个平面，这个平面的右边假设有一些发光的物体，这些发光的物体会发出各种各样的光会穿过这个平面。我们前面说平面右边的东西可以忽略，而只关心平面左边的信息就可以。也就是说，对这个平面上的任意一个点，我们能知道它任意的一个方向就可以了。

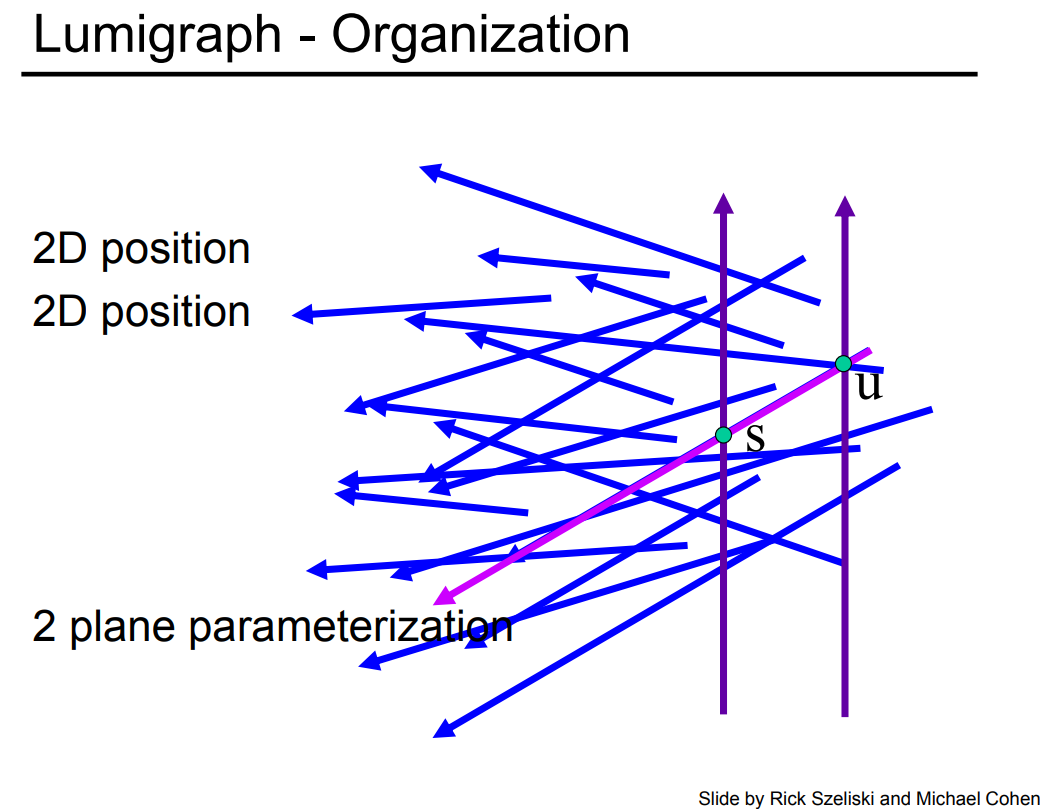
那么我们也可以用两个相互平行的平面来定义任何一个光场，只需要在两个平面上各自任取一个点即可。

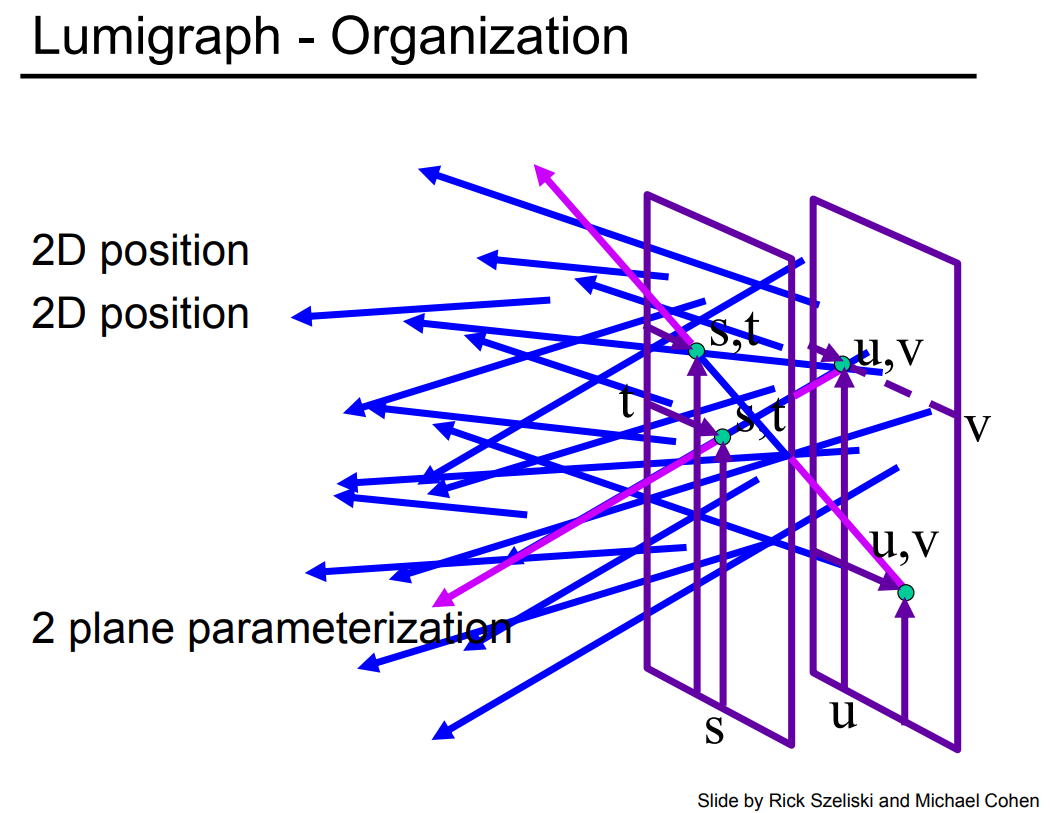
因此，在光场里面平时大家会用到 uv 和 st 的概念，也就是对光场参数化的过程，因为光场本质上就是一个四维的函数，就取决于我们怎么描述这个四维函数而已。那么对于两个平面来说，假设我们知道发光的物体在右边（确定了光照的方向），那么平面上任意的两个点的连线就能找到一条光线，之后确定这条光线的值并记录下来。重复上面的步骤，我们只要找到所有的 uv，所有的 st 它们的组合就可以了。到此为止，我们基本上就把光场的概念说清楚了。

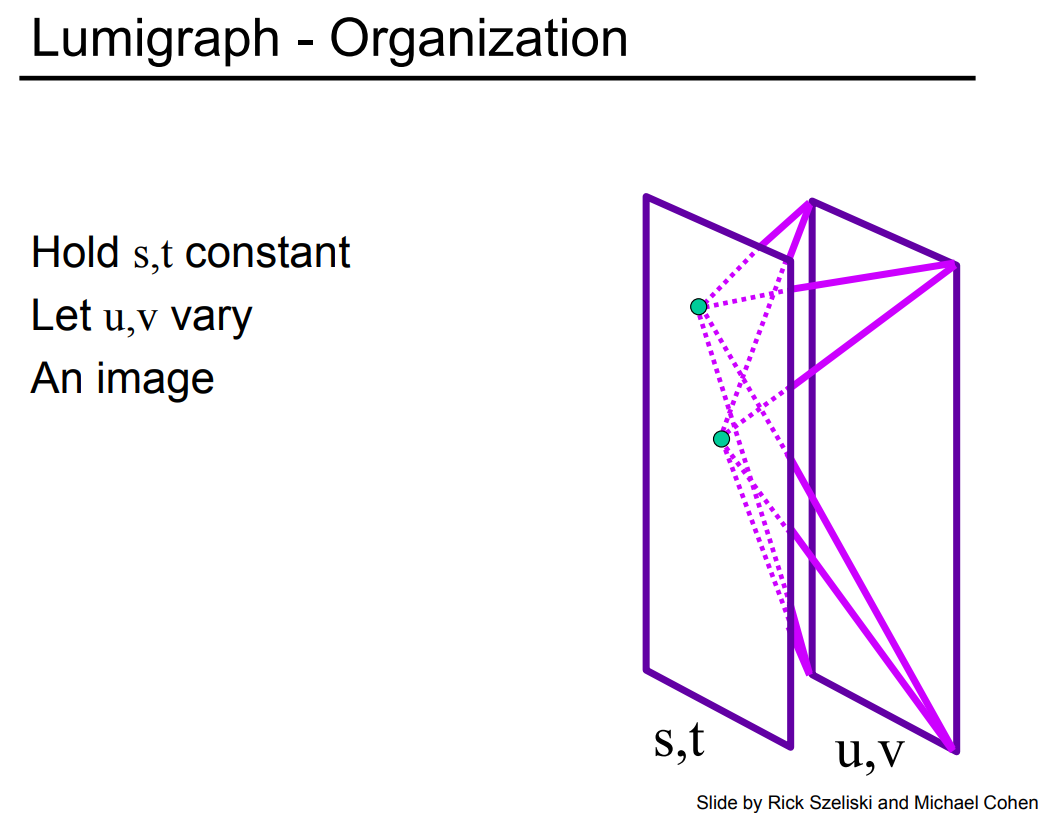
我们再来看看对两个平面这种参数化方式的两种不同的理解方式。我们可以在 st 上取一个点，然后看所有的 uv 长什么样。我们通过下面这张图来理解这句话。

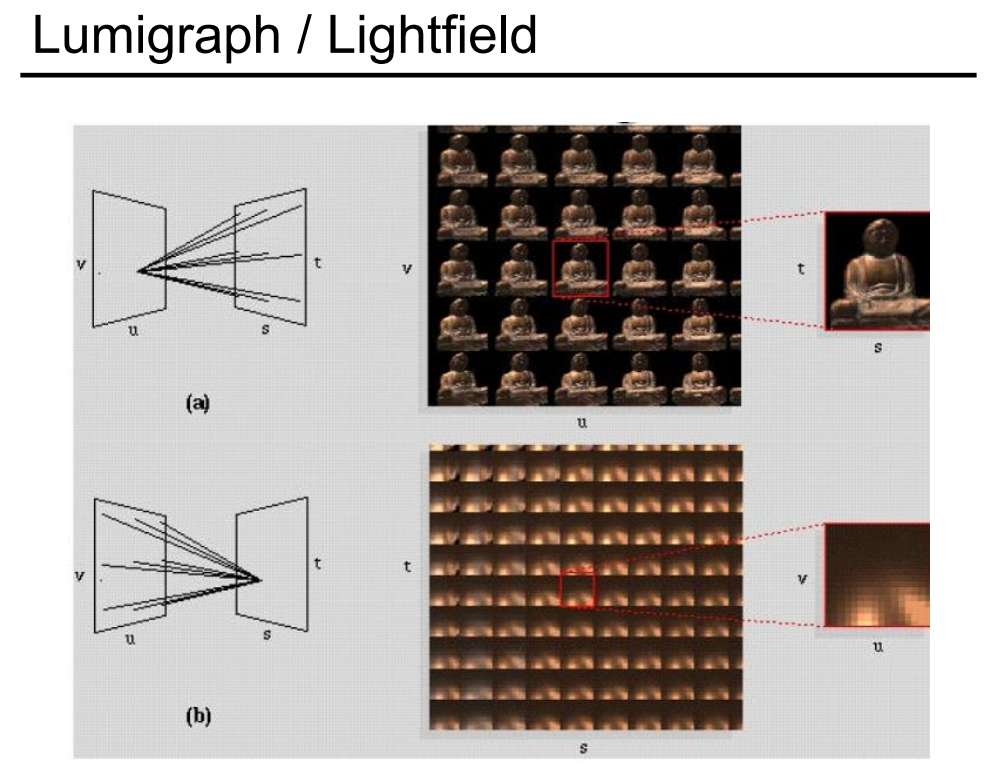
我们记录的光场，就相当于是在 st 上取一个点，然后 uv 上取一个点，再把它们连起来。如果我们在 uv 上面取一个固定的点，然后再去看向所有的 st 平面上的点，这就好像是没有光场一样。因为我们在 uv 上取一个点，然后看向这个世界，这个世界右边都是我们不关心的东西，也就好像一个针孔相机所能看到的东西，因此每一个点我们都能看到一个完整的图，只不过是以不同的角度看向这个世界。相对难以理解的是，我们固定 st 上的一个点，然后再往 uv 平面上去看，整个世界还是在 st 平面的右边，我们反过来想，也就是在 uv 上的每一个点都看向 st 上的同一个点，这样的话我们看的是同一个点只不过是从不同的角度去看，那么我们就能看到各个角度不同高光的效果。或者我们也可以理解成，当摄像机拍了一张图之后，一个像素上存的是 Irradiance 的信息，那么通过这种方式就能把像素上的 Irradiance 给展开成为 Radiance，我们能看到打到任何一个像素上不同方向的光到底是什么。

斯坦福大学做出来摄像机矩阵就对应了我们上面讲的第一种理解。

我们其实更关心的是另外一种。在自然界中，有一些昆虫例如苍蝇，它们的眼睛称之为复眼。苍蝇眼睛的成像原理其实就是在成像一个光场。还是从刚才的角度来说，我们盯着原本正常拍出来的照片来看，照片上的任何一个像素它记录的是 Irradiance，Irradiance 不区分来自各个方向的光，然后把它们都平均在一块儿。对于光场的另外一种理解方式，我们把上图中的 lenslet 当作某一个像素，那么对于最左边的像素来说，它接受到的光有来自于左边的蓝色、来自于正上方的绿色、来自于右边的红色。如果是普通的相机，我们就把这个像素给记录下来了，这个记录的结果就是蓝色、绿色和红色的平均。如果我们有办法能把它们都分开，也就是光线打到像素上之后不立刻记录它，而是把这个像素变成某个小透镜，这个小透镜的作用就是把来自各个方向的光给分到不同的位置上去，实际的感光元件放在底下，经过分光这一步操作之后，我们就能把原本打在像素上的各个方向的光分别记录在不同的位置。这就相当于，我们记录的不再是一个像素的 Irradiance 了，而是记录往各个方向看过去的 Radiance，这也正是光场摄像机的基本原理。我们看着一个像素，其实相当于看着穿过这个像素的不同方向的光。

# Light Field Camera

光场的原理我们已经清楚了，利用这个原理就能做出光场摄像机。光场相机中用到了微透镜，也就是把一个像素替换成一个透镜，然后让这个透镜可以把来自于不同方向的光分开并记录下来。光场相机最重要的功能就是支持后期的重新聚焦。使用光场相机我们可以先拍张照片，然后在考虑聚焦或者别的一些问题，例如调整光圈大小等等。

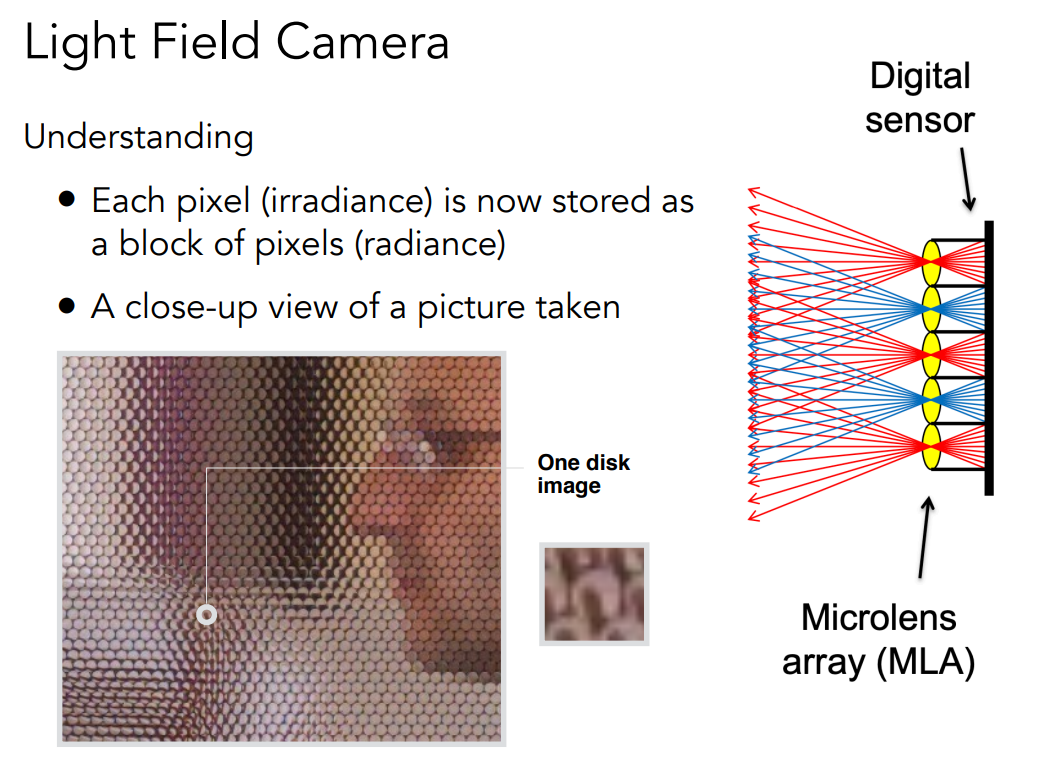
光场相机的原理就是光场的原理。原本我们的成像平面是在上图的透镜处，在普通的相机里，这就是我们的像素。任何一个像素它会接收到来自各个方向上不同的光，然后把它们平均起来，也就是 Irradiance。光场相机的原理就相当于把原本的这些像素换成了微透镜，这些微透镜就会把来自个方向上的光给分散到不同的方向上去，我们在后面把这些光线给记录下来，也就是说把感光元件往后面拿一点点，让不同方向上的光经过透镜之后正好分散在一片区域上。光场相机和普通相机的区别就在于，原本我们只需要记录一个像素，现在我们要记录一块像素。光场相机照出来的最原始的图中，原本一个像素变成一个圆，任何一个圆内部如果平均起来就是传统相机的结果，如果考虑在这个圆的内部各个像素在干些什么，那么它们实际上记录的就是光线各个不同的方向。光场相机做到了把来自各个方向上不同的光都记录下来。我们观察上图中透镜的位置，不同的透镜对应不同的位置，不同的透镜又能接受到不同方向上来的光并且把它们存起来，从这些透镜往左边看可不就是一个光场吗？

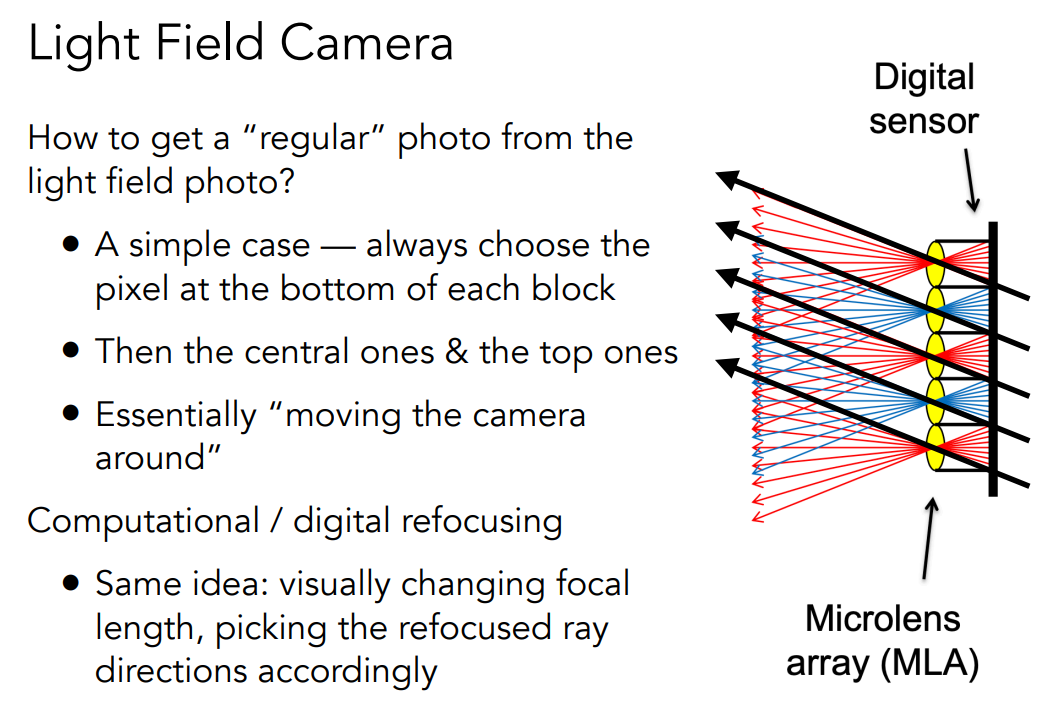
我们有了一张光场相机拍出来的最原始的图，但是我们最后想要一个普通的相片该怎么办？一个很简单的办法，原本用光场相机之前，这些微透镜都是像素。如果我们把每个微透镜后面的都选一条同一个方向的光线，然后我们把每个得到的结果记录在对应像素上，也就是说现在的透镜就只对应一个值了，那么我们就能得到一张原始的照片。这张照片拍出来的效果就好像是我们把相机放在某一个位置然后往这个特定的方向去看。也就是说，有了光场之后，我们就能虚拟地移动摄像机的朝向让它向着指定的方向去看。这里我们没有具体的说动态的重新聚焦怎么做，但是重新聚焦也是伊一样的道理，因为我们拥有整个光场，那么要想把一个焦平面移动的非常远或者非常近，在移动的过程中就对应着这些光线应该如何变化，那么我们就在光场中去查询更新后的光线，也就是按需在光场里面去取就可以了。这和我们移动相机的位置理论上是一模一样的，也就是中间我们要进行一些计算，算出来我们应该取哪些方向。

总结起来，为什么这些功能得以实现，正是因为光场相机记录了整个光场的信息，整个光场就是所有进入到相机里的所有的信息，包括位置和方向。但是光场相机本身也存在一些问题，例如光场相机通常都有分辨率不足的问题，这是因为我们改变了成像平面之后，我们现在可能要用 100 个像素去记录原先一个像素的信息，因为我们把不同的方向分开了。现在胶片的分辨率就变成了空间上的分辨率，即原本照片的分辨率乘以方向上的分辨率。现在方向上记录的信息多，那么在照片本身记录的分辨率就会低，所以这种方式对胶片分辨率的要求非常高，自然而然这种方式就会造成高成本。高成本不仅体现在为了让光场相机达到和以前一样的照片分辨率，那么就得用超级高分辨率的胶片。其次就是微透镜是一种超级精密的仪器，实现起来会非常困难。这就造成了光场相机的高成本。这里我们再次体会到整个计算机图形学都存在对各种方面的权衡，如果提升了其中的一块，那么另外一块可能就会受到影响。